OBSAH:
11-12. Sommerfeldovo chápanie elektromagnetizmu - alebo kedy sa konečne urobí poriadok
s Gaussovou CGS-sústavou? (1-2)
13. Mohol iba jeden kilogram uránu zničiť Hirošimu?
14. Ako funguje mikrovlnová rúra - "mikrovlnka"?
15. Fyzikálne úlohy a ich postavenie pri štúdiu fyziky.
11. Sommerfeldovo chápanie elektromagnetizmu – alebo kedy sa konečne urobí poriadok s Gaussovou CGS-sústavou? (1)

Arnold Johannes Wilhelm Sommerfeld
(1868-1951)
V tomto roku uplynie 140 rokov od narodenia veľkého nemeckého teoretického fyzika a vysokoškolského pedagóga Arnolda J. W. Sommerfelda. Možno že mi nepatrí písať biografie slávnych fyzikov, ale v jeho prípade robím to preto, lebo Sommerfeld ako vynikajúci teoretický fyzik si uvedomoval, že vo fyzike treba predovšetkým merať a že žiadna teória nie je k ničomu, ak nie je overená a využitá v praxi. Sústava jednotiek CGS, ktorá sa v jeho čase vo fyzike používala, sa ale k meraniu – hlavne v elektromagnetizme – hodí najmenej.
Sommerfeld sa narodil v Königsbergu (terajší Kaliningrad), jeho otec bol praktický lekár zaujímajúci sa o prírodné vedy. Königsberg bol Mekkou matematickej fyziky a filozofie. Sommerfeld získal vynikajúce matematické a fyzikálne vzdelanie doma, na Univerzite Albertina, kde pôsobili takí veľkí pedagógovia a vedci ako Franz Neumann (1798-1894), Carl G. J. Jacobi (1804-1851) a Friedrich W. Bessel (1784-1846). Študoval priamo u Davida Hilberta, Ferdinanda von Lindemanna a Adolfa Hurwitza. Promoval v roku 1891 prácou Spontánne funkcie v matematickej fyzike (Die willkürlichen Functionen in der mathematischen Physik). Vedecky ho ovplyvnil Emil Wiechert, s ktorým neskôr nadviazal priateľstvo.
V roku 1893 odišiel na Univerzitu v Göttingene, kde sa stal asistentom na mineralogickom ústave, jeho hlavným záujmom však a naďalej zostala matematika a matematická fyzika. V roku 1894 sa stal asistentom matematika Felixa Kleina, ktorý bol jeho vedeckým vzorom a pod jeho vedením vypracoval habilitačnú prácu Matematická teória difrakcie (Matematische Theorie der Diffraction) na základe ktorej sa stal privátnym docentom, s Kleinom vydal knihu Teória zotrvačníkov (Treorie des Kreisels) a bol ním poverený písať rôzne príspevky o fyzike do Encyklopédie matematických vied.
V roku 1900 dostal Katedru technickej mechaniky na vysokej škole technickej (RWTH) v Aachene a v roku 1906 miesto profesora teoretickej fyziky na Univerzite v Mníchove, kde postupne vybudoval význačné centrum teoretickej fyziky. Hoci mu boli ponúkané rôzne renomované katedry, v Mníchove zostal celý zvyšok svojho života, s výnimkou cesty do USA, kde na Univerzite vo Wisconsine pôsobil ako hosťujúci profesor v rokoch 1922/23 a ako vysokoškolský profesor vykonal v rokoch 1928/29 cestu do Ázie (India, Čína, Japonsko) a znovu do USA. V roku 1935 išiel do dôchodku, no ako emeritný profesor prednášal až do roku 1940. Dlhé spory viedol pri výbere svojho nástupcu: Sommerfeld na to miesto uprednostňoval Wernera Heisenberga, narazil však na odpor stúpencov „Deutsche Physik“, ktorí nakoniec – podľa Sommerfelda – vybrali zo všetkých do úvahy pripadajúcich adeptov toho najhoršieho. Po skončení nacionálno-socialistickej diktatúry v roku 1945 sa opäť pokúšal presadiť v centre teoretickej fyziky svojho nástupcu, ktorý by pokračoval v tradícii jeho školy. Navrhoval medzi inými aj Wernera Heisenberga, Karla Bechera, Hansa Betheho a Carla Friedricha von Weiszäckera, všetci však túto funkciu odmietli.
Sommerfeld zomrel v roku 1951 na následky autonehody.
Spolu s Maxom Planckom, Albertom Einsteinom a Nielsom Bohrom Sommerfeld patril k vedcom, ktorí na začiatku 20. storočia formovali teoretickú fyziku a fyziku vôbec na oporných stĺpoch kvantovej mechaniky a teórie relativity. Bol významný ako vedec, ale aj ako vysokoškolský profesor. Jeho vedecký príspevok možno bol menší pri formulácii nových prevratných fyzikálnych teórii, o to väčší bol pri využití moderných matematických metód na riešenie fyzikálnych a technických problémov. Jedným z dôležitých príspevkov k rannej kvantovej teórii bolo dopracovanie Bohrovho atomového modelu tak, že dokazal vysvetliť aj jemnú štruktúru spektrálnych čiar vodíka (Bohrov-Sommerfeldov model atómu). Zaviedol pri tom konštantu jemnej štruktúry alfa ≈ 1/137. Okrem toho rozvinul teóriu Röntgenového žiarenia, vylepšil Drudeho teóriu vodivostných elektrónov použitím kvantovej mechaniky (Drudeho – Sommerfeldova teória) a vypracoval obsiahlu teóriu zotrvačníkov.
Sommerfeld bol prvým fyzikom, ktorý prijal Einsteinovú špeciálnu teóriu relativity, používal ju v praxi a tak prispel k jej presadeniu. Zaoberal sa tiež vývojom hydrodynamických klzných ložísk a zaviedol po ňom pomenované Sommerfeldovo číslo ako mieru zaťaženia ložiska.
Mnohí fyzici 20. storočia, sčasti nositelia Nobelovej ceny pochádzali zo známej Sommerfeldovej školy – centrum teoretickej fyziky, boli asistentmi, doktorandi, alebo sa občasne zúčastňovali na jeho prednáškach. Táto škola významne ovplyvnila rozvoj vedy, predovšetkým kvantovej mechaniky, a to kvalitou práce ako aj katedrami, ktoré v Nemecku a v USA vznikli. Dvaja z jeho žiakov – Werner Heisenberg a Wolfgang Pauli – zásadne ovplyvnili rozvoj kvantovej mechaniky. Ďalší z jeho žiakov boli nositelia Nobelovej ceny okrem iného Peter Debye, Hans Bethe, Isidor Isaac Rabi a Linus Carl Pauling.
Sommerfeld ovplyvnil vedecké bádanie aj ako autor odborných monografií. V roku 1919 vyšla prvý raz jeho kniha Stavba atómov a spektrálne čiary (Atombau und Spektrallinien), ktorá rozšírená vychádzala v ďalších rokoch a odzrkadľovala v tomto období rýchly rozvoj atómovej fyziky. Bola to na dlhé obdobie jedna z najdôležitejších publikácii, ktorá sprístupňovala experimentátorom teoretické výsledky mladej kvantovej mechaniky a pri výchove študentov zohrala vynikajúcu úlohu.
V období rokov 1943 – 1947 napísal svoje vrcholné pedagogické dielo, šesťdielne Prednášky z teoretickej fyziky (Vorlesungen über theoretische Physik) u nás známe hlavne z ruských prekladov. Tretí diel tohto kurzu venoval Sommerfeld elektrodynamike, kde definitívne zavrhol Gaussovu CGS-sústavu fyzikálnych jednotiek. Ako vynikajúci teoretik, so zmyslom pre potreby fyzikálnej práce videl, že táto sústava bude v nasledujúcich rokoch neudržateľná a od rokov 1933/34 prednášal elektrodynamiku v MKSQ sústave, ktorú sám navrhol a ktorá s malými úpravami bola základom pre SI-sústavu. V Úvahe 12 bude okrem iného uvedený preklad časti predslovu k jeho „Elektrodynamike“ a tie výhrady, ktoré možno vzniesť proti CGS-sústave.
Sommerfeld bol od roku 1908 členom Bavorskej akadémie vied a od 1926 Fellow of Royal Society v Londýne. V roku 1917 mu bola Pruskou akadémiou vied udelená Helmholtzova Medaila a v roku 1931 Nemeckou fyzikálnou spoločnosťou (Deutsche Physikalische Gesellschaft) Max-Planck-Medaila.
Želám Vám pekný deň! Autor
7. 8. 2008
12. Sommerfeldovo chápanie elektromagnetizmu – alebo kedy sa konečne urobí poriadok s Gaussovou CGS-sústavou? (2)
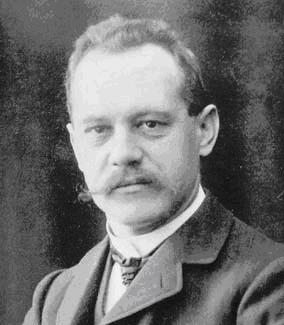
Arnold Johannes Wilhelm Sommerfeld
(1868-1951)
Tak budeme pokračovať v úvahách o Sommerfeldovi a o CGS-sústave! Chcel by som sa vopred ospravedlniť za štýl prekladu predslovu k Sommerfeldovej „Elekrodynamike“, ktorý znie trochu archaicky, ale aj Sommerfeldov originál je archaický. Okrem toho sa ospravedlňujem za vypisovanie niektorých gréckych písmen vo vzorcoch latinkou, ale použitý textový editor iný spôsob neumožňuje.
Nuž, nech teda hovorí Herr Professor Sommerfeld!
........ Všade, bez výnimky budeme venovať veľkú pozornosť rozmerom veličín, ktoré charakterizujú pole. Odmietame názor Plancka, podľa ktorého otázka o skutočnom rozmere fyzikálnej veličiny nemá zmysel; v §7 svojich prednášok o elektrodynamike Planck tvrdí, že podobné otázky nemajú väčší zmysel, ako otázka o „reálnosti“ názvov vecí. My práve naopak a naviac, vidíme fundamentálny rozdiel napríklad medzi „silovými veličinami“ (Intensitätsgrößen) a „kvantitatívnymi veličinami“ (Quantitätsgrößen), ktoré berieme za základ Maxwellových rovníc, a tento rozdiel už bol konzekventne posúdený vo vynikajúcich učebniciach Mie-ho. Faradayov-Maxwellov zákon elektromagnetickej indukcie svedčí o tom, že silovou veličinou popri intenzite elektrického poľa E je aj magnetická indukcia B; práve B a nie H by si zaslúžilo názov intenzita magnetického poľa. Veličinu H podobne ako D, by bolo najlepšie nazvať „budenie“ (Erregungsgröße). Podobne ako veličina div D udáva veľkosť objemovej hustoty elektrických nábojov, div H by mala udávať hustotu magnetického náboja (!). Hertzovo rozlišovanie medzi „skutočnou“ (wahrer) a „voľnou“ (freier) elektrinou neplatí, pretože podľa rozmeru, div E neudáva náboj, ale divergenciu siločiar. To isté možno povedať aj o „skutočnom“ a „voľnom“ magnetizme. Na druhej strane div B sa vždy a všade rovná nule.
Súčasne s H a D, kvantitatívnymi veličinami sú aj prúdová hustota j, elektrická polarizácia P a magnetizácia M. Energetické veličiny sú vždy súčinom kvantitatívnych a silových veličín, napríklad (1/2)D·E; (1/2)H·B; J·E; E × H. Spolupatričnosť veličín E a B ako aj H a D jednoznačne dosvedčuje teória relativity, kde na jednej strane veličiny cB a –iE (c – rýchlosť svetla vo vákuu a „i“ je imaginárna jednotka – pozn. autora) a na druhej strane H a –icD sa spájajú do šesťvektora (do antisymetrického tenzora). Prvý označíme F a nazveme tenzorom poľa (Feldtensor) a druhý f, nazveme tenzorom budenia (Erregungstensor).
Rozhodujúcim pre plodotvornosť rozmerových úvah je zavedenie ďalšej, od mechanických jednotiek nezávislej štvrtej elektrickej jednotky. Takúto jednotku Q nazveme jednotku náboja a z praktických dôvodov ju môžeme (ale nemusíme) stotožniť s jednotkou coulomb. Vyhneme sa tak „Prokrustovmu lôžku“ CGS-jednotiek v ktorom sa elektromagnetickým jednotkám nanucujú známe neprirodzené veľkosti. Keďže sa definitívne vzdávame nádeje na mechanický výklad elektrických veličín, budeme náboj považovať za principiálny „prapojem“, ktorý ma právo na vlastnú meraciu jednotku. O „elektrostaticky“, alebo „elektromagneticky“ meraných nábojoch budeme hovoriť iba predbežne a to z historických dôvodov. Špeciálne zvolenou jednotkou náboja Q = 1 coulomb (C) možno potom elektrický prúd vyjadriť pomocou všeobecne používanej jednotky 1 Ampér = 1 C/s.
Ako mechanické jednotky budeme používať G. Giorgi-ho sústavu jednotiek: dĺžka meter m, kilogram hmotnosti kg a sekundu s. Jednotkou energie bude 1 erg, alebo „veľký erg“ = 1 Joule (a to bez potreby pridávania dekadických súčiniteľov), jednotka výkonu je 1 erg/s = 1 Watt. Ale aj pre elektrické jednotky volt, ohm, farad, henry nie sú potrebné žiadne dekadické súčinitele: menovite 1 volt = 1 erg/C, 1 ohm = 1 erg.s/C2, 1 farad = 1C2/erg, 1 henry = 1 erg.s2/C2. (Treba pripomenúť, že 1 erg = 10-7 joule (J) je jednotka práce, alebo energie v CGS-sústave – pozn. autora).
Naopak pri magnetických jednotkách, ktoré sú šité na mieru CGS-sústavy, treba pri prepočte jednotky gauss (pre magnetickú indukciu B) a oersted (pre intenzitu magnetického poľa H) priradiť dekadické súčinitele, ako to uvidíme v §8 (dnes používaná jednotka 1 Tesla (T) = 104 gaussov pre magnetickú indukciu B a 1 A/m = 4×pi/103 oerstedov (pi = 3,14159..... je Ludolfovo číslo) pre intenzitu magnetického poľa H – pozn. autora).
Z už zavedených hustôt energie (1/2)D·E; (1/2)H·B; J·E; vypadne štvrtá jednotka Q, čo je samozrejmé. Rozmer hustoty energie je priamo erg/m3 a rozmer toku energie za sekundu E × H je erg/(m2.s).
Pri našom rozmerovom rozlišovaní medzi intenzitnými a kvalitatívnymi veličinami, dielektrická konštanta (permitivita – pozn. autora) a permeabilita musia byť zrejme rozmerové veličiny a ani pre vákuum nemôžu mať hodnotu 1. Ak vyberieme µ0 a epsilon0 v súhlase s elektrotechnickými požiadavkami a praxou, ocitneme sa vo výhodnej pozícii, takej, že požiadavkám na „racionálne jednotky“ možno bez ťažkosti vyhovieť. Stačí v súlade s medzinárodnými požiadavkami položiť
µ0 = 4× pi×10-7 (ohm.s/m = H/m)
a epsilon0 sa vypočíta zo vzťahu epsilon0×µ0 = 1/c2, čo bolo spoľahlivo overené Hertzovými pokusmi. Pri takomto výbere epsilon0 a µ0 vypadne 4×pi zo všetkých rovníc, kam nepatrí, napr. z Poissonovej rovnice, alebo z výrazov pre energiu, z Poyntingovej rovnice (Poyntingova veta – pozn. autora). Naopak 4×pi vstúpi do tých vzťahov tam, kam patrí, ako je Coulombov zákon, alebo do výrazu pre kapacitu guľového kondenzátora. Vyhneme sa takto pochybnej ceste, ktorú podstúpil rozčarovaný Lorentz vo svojom encyklopedickom článku v záujme racionalizácie, menovite, keď sa pokúšal do definície elektrického a magnetického náboja zahrnúť faktor √(4×pi).
Ak prijmeme tento nami navrhovaný postup, zistíme, že odmocnina z pomeru µ0 a epsilon0 má rozmer odporu. Táto veličina je známy „vlnový odpor vákua“ (dnes sa táto veličina nazýva „vlnová impedancia voľného priestoru (vákua) Z = √(µ0/epsilon0) = µ0c = 376,73 ohmov" – pozn. autora), sa bude objavovať ako faktor všade tam, kde vektory E a H bude treba vyjadrovať výrazmi s rovnakými rozmermi (to sa deje práve v CGS-sústave – pozn. autora). Veličina vystúpi aj v teórii relativity vo vzťahu medzi tenzorom budenia (Erregungstensor) f a tenzorom poľa (Feldtensor) F, ktorý pre všetkých šesť komponent nadobúda jednoduchý tvar
f = √(epsilon0 /µ0) ×F.
Všetkým týmto, v posledných rokoch do omrzenia pertraktovaným otázkam jednotiek, rozmerov a racionalizáciám sa v prednáškach budeme venovať podľa možnosti len krátko; na niektorých miestach však budeme od čitateľa očakávať, že sám sa presvedčí o rozmerovej správnosti výrazov. Pri numerických výpočtoch sa naša sústava jednotiek MKSQ bez výnimky osvedčuje, pretože je priamo zviazaná so zákonnými jednotkami volt, ampér, atď. Otázku, či sústavu možno odporúčať aj v atómovej fyzike nebudeme posudzovať. Kvôli uľahčeniu prechodu na zatiaľ v iných častiach používanú Gaussovu sústavu (epsilon0 = µ0 = 1), posúdime v §9 Cohnovu sústavu, ktorá sa podľa nášho chápania zakladá na piatich jednotkách MKSQP (P – jednotka magnetického pólu).
Sommerfeld na prednáške
Čarovná jednoduchosť a krása Maxwellových rovníc, ktoré sa obzvlášť jasne vynímajú v ich relativistických formuláciach pre vákuum, vedú nás k presvedčeniu, že tieto rovnice spolu s gravitačnými rovnicami musia byť východiskom k všeobecnej svetovej geometrii. Z toho plynúce formulácie, ktoré sú zatiaľ v štádiu výskumu budú sumarizované v §37. Prekvapujúco jednoduchá predstava všeobecnej teórie relativity v §38 sa zakladá na odvodení Schwarzschildových čiarových elementov, ktoré mi láskavo poskytol W. Lenz. Z toho sa dajú prostrednictvom astronomických pozorovaní bezprostredne, bez tenzorového počtu, získať tri dôsledky teórie.
Rukopis tohto zväzku spracoval H. Welker z prednášok zimného semestra 1933/34, kedy som sa v prednáškach prvý raz vzdal CGS-sústavy jednotiek a prešiel som na všeobecný systém štyroch jednotiek MKSQ. Pri definitívnom spracovaní I. a II. dielu ma stálymi radami podporoval Profesor J. Jaumann, ktorý svojimi skúsenosťami z elektrotechniky veľmi zvýšil úroveň týchto zväzkov. Za kritické pripomienky a rady na zlepšenie ďakujem pánom P. Mannovi a E. Goraovi ako aj kolegovi F. Boppovi. Pri korektúre podobne ako pri predchádzajúcich zväzkoch so mnou spolupracoval Dr. W. Becker.
Mníchov, v apríli 1948 Arnold Sommerfeld
Tak toľko Sommerfeld! Samozrejme nie všetko možno zo Sommerfeldových predstáv prijať, ale to, čo je neadekvátne, jeho teóriu antagonisticky nezaťažuje.
Rozhodnutím 11. generálnej konferencie pre miery a váhy (CGPM) v roku 1960 sa medzinárodne prijala nová sústava meracích jednotiek pod názvom „Medzinárodná sústava jednotiek (Systéme International d´Unités)“ so skratkou „SI“. Podľa uznesenia vlády ČSSR č. 7/1974 bola prijatá aj u nás. Oproti CGS-sústave to bol veľký pokrok. Postupne k dohode pristupovali aj iné štáty a v priemyselnej praxi a v experimentálnych vedeckych disciplínach sa to všade chápalo ako veľký prínos.
Komu SI-sústava od začiatku nevyhovovala, boli to teoretickí fyzici! Tí často argumentujú tým, že Coulombov zákon má v SI-sústave zložitý koeficient k = 1/(4×pi×epsilon0), zatiaľ čo v CGS-sústave k = 1. No boooože! A to, že ich rovnice sa hemžia koeficientami 4×pi, 1/c, prípadne 1/c2 to im nevadí. Iní argumentujú, že sa z rovníc elektromagnetizmu vytratila rýchlosť svetla c, ale to vôbec nie je pravda, pretože epsilon0 = 1/(µ0c2) a µ0 je dané z definície. Teda tam, kde je epsilon0, tam je aj c, presnejšie 1/c2. Okrem toho dúfam, že sa s teoretikmi zhodneme, že základný zákon elektrostatiky nie je Coulombov zákon, ale Gaussov zákon, a v ňom hneď majú naviac 4×pi, čo SI sústava nemá. Skutočne, stoja ich argumenty za tých 1/(4×pi×epsilon0)? Teoretickí fyzici by si nemali myslieť, že v tej medzinárodnej komisii, ktorá deklarovala SI-sústavu, sedeli sami hlupáci a že neočakávali ich neoprávnené budúce výhrady a protiargumenty. Mali by si však uvedomiť, že CGS sústava je absolutne nevhodná na praktické aplikácie fyziky a prejaviť viac empatie.
Ak si dnes, teda 48 rokov po zavedení SI-sústavy, otvoríte editor Google a pozriete nemecké, alebo aj švajčiarske stránky s názvom "Theoretische Physik: Elektrodynamik“, s hrôzou zistíte, že Učebnice a skriptá daného predmetu používané na slávnych nemeckých univerzitách, niektoré napísané rukou a iba na jar tohto roku (2008!) sú v CGS-sústave!!! A to nie výnimočne, to je takmer pravidlo. Neviem, či je to benevolencia nemeckej štátnej správy, alebo jednoducho arogancia teoretických fyzikov – veď Nemecko k tejto dohode o SI pristúpilo ešte pred nami. Nemci teda ignorujú svojho slávneho predka, vysoko-školského pedagóga a vedca Sommerfelda, ktorý bojoval celou váhou svojej autority a osobnosti proti plesnivej, neadekvátnej a nepraktickej sústave jednotiek CGS.
Takže v Nemecku sa v 21. storočí na univerzitách učia študenti elektromagnetizmus v sústave fyzikálnych jednotiek, v ktorej štyri základné vektory elektromagnetického poľa teda E, D, B, H majú jeden, rovnaký rozmer (všetko sa meria, lepšie povedané udáva, v čudných jednotkách – s rozmerom m-1/2.kg1/2.s-1).
Učia sa elektromagnetizmus v sústave jednotiek, v ktorej elektrický náboj má rozmer mechanických jednotiek, konkrétne m3/2.kg1/2.s-1!?
Pýtam sa, že čo je to za sústava, v ktorej nemožno numericky jednoducho vypočítať ani len objemový tok elektromagnetického výkonu, teda Poyntingov vektor E×H, ktorý v CGS-sústave treba počítať z výrazu cE×H /(4×pi) a nikto nevie, v akých jednotkách treba vektory poľa zadať (ale určite nie v takých, v akých sa dnes polia merajú, c tam samozrejme vystupuje v cm/s)!?
A čo je to za sústava, v ktorej sa kapacita kondenzátorov a rovnako aj indukčnosť cievok udávajú v centimetroch!?
Čo je to za sústava, ktorá dnes – keď elektromagnetické vlny a ich toky sa šíria všetkými smermi v obrovských hustotách a pri všetkých možných frekvenciách – nepozná veličinu „vlnová impedancia voľného priestoru (vákua) Z ≈ 377 ohmov“, resp. pozná ju ako nejaké bezrozmerné číslo? Túto veličinu (ani v sústave SI) teoretici takmer nespomínajú a pritom je to pre prax veľmi dôležitý pomer absolútnych hodnôt vektora intenzity elektrického poľa E(V/m) a k nemu ortogonálneho vektora intenzity magnetického poľa H(A/m) vo voľnom priestore (vo vákuu), pritom energia tečie v smere kolmom na tieto dva vektory s výkonovou hustotou E×H vo W/m2. Vlnovú impedanciu Z = E/H = µ0c (ktorá je vlastne tak ako rýchlosť svetla c, prírodnou konštantou ) dokáže dnes merať každý lepšie vybavený rádioamatér, a tak je napríklad schopný overiť hodnotu rýchlosti svetla c.
Niekedy ma napadá otázka: komu „CGS-elektromagnetizmus“ dnes vlastne slúži a či to nie je len samoúčelná hračka pre teoretikov. Ja ho považujem iba za prostriedok zavádzania a zneisťovania študentov študujúcich elektromagnetizmus. U nás CGS-sústavu zakázali ešte komunisti (aspoň niečo urobili dobre), ale u priateľov teoretikov stále vyvoláva nostalgiu, u niektorých, hlavne ak študovali na Západe (čiastočne aj v USA), dokonca frustráciu.
Nikto ma nepresvedčí, že študent, ktorý absolvuje „CGS-elektromagnetizmus“, potrebuje iba nejakú prevodovú tabuľku a bude bez problémov pracovať v „SI-elektromagnetizme“. Nie je to pravda, pretože tento prechod nie je jednoduchá konverzia čísel, resp. konštánt, ako je to napr. v mechanike. Je to otázka zmeny filozofie a študent-chudák sa to musí všetko naučiť znovu, a vysporiadať sa s nadobudnutým zaťažením CGS-sústavou. Prejsť z CGS-sústavy do SI-sústavy v elektromagnetizme je rozhodne obtiažnejšie ako prepočítať palce na centimetre a práve takýto mylný prepočet v NASA spôsobil haváriu istého projektu. Želám Vám dobrý deň a netrápte sa tým – je to zbytočné! Autor
7. 8. 2008
13. Mohol iba jeden kilogram uránu zničiť Hirošimu?
Death am I, and my present task Destruction. (Bhagavad Ghita)
V týchto dňoch je výročie kataklizmy, ktorá sa udiala nad Hirošimou a Nagasaki v prvých augustových dňoch roku 1945, kedy tam vybuchli dve atómové bomby, pričom zomrelo viac ako stotisíc ľudí. Každá z bômb mala – podľa údajov agentúr – okolo jedného kilogramu štiepneho materiálu izotopu uránu U235. Táto udalosť, o ktorej nikto neveril, že sa dá uskutočniť, otriasla obyvateľstvom planéty. Tí pragmatickejší si začali klásť otázky: Je skutočne možné, že v kilograme hmotnosti látky sa skrýva taká obrovská energia (nie len v uráne, ale aj v ľubovoľnej inej, nerádioaktívnej látke)?

Explózia „Trinity“ 1,6 milisekundy po detonácii.
Mrak je priemeru asi 200 metrov.
Explózia „Trinity“ o 9 milisekúnd neskôr.
Žiaľ, dnes z toho, čo sa dialo po roku 1945, v období studenej vojny vieme, že to, čo zažila Hirošima a Nagasaki, boli iba malé ukážky tej zničujúcej energie, ktorú hmota ukrýva. Hovorí sa, že tvorcovia prvej atómovej bomby, účastníci na Projekte "Manhattan" v Alamogordo, Los Alamos National Laboratory v New Mexico, USA , pred odpálením "Trinity" si ani neboli tak celkom istí, či po odpálení bomby nedôjde k všeobecnej reťazovej reakcii, ktorá sa nezastaví, kým nezničí celú zemeguľu. Po výbuchu bomby boli otrasení aj takí „tvrdí“ fyzici ako Oppenheimer, Fermi, alebo Feynman a pre zostatok života viacerí z nich mali psychické problémy.
J. Robert Oppenheimer Enrico Fermi Richard Feynman
riaditeľ Projektu Manhattan
Nuž, pozrime sa, čo sa v takom atómovom jadre skrýva. Chceme odpoveď na jednoduchú otázku: Aká energia sa rádovo uvoľní pri výbuchu atómovej bomby, v ktorej ako štiepny materiál je 1 kilogram uránu U235. Potrebné vedomosti na zodpovedanie tejto otázky získate v učebnici „Elektromagnetizmus“ umiestnenej na tejto webovej stránke:
Jadrá ťažkých atómov majú náboj rozložený približne rovnomerne v guľovom objeme s polomerom a, s obrovskou objemovou hustotou ro = 1,33.1025 C/m3. Elektrická energia W guľového náboja (jadra atómu U235) je daná výrazom
W = 3Q2/(20×pi×epsilon0×a),
kde Q je celkový náboj jadra, pi = 3,14159..... je Ludolfovo číslo. V jadre U235 je 92 protónov, každý protón s nábojom e = 1,602.10-19 C a zvyšok – do 235 – sú neutróny. Ak sa jadro rozpadne na približne rovnaké časti (čo možno pri ťažkých, nestabilných jadrách dosiahnuť „ťuknutím“ jadra pomalým neutrónom), ukazuje sa, že súčet energii dvoch polovičných jadier je menší ako je energia pôvodného jadra. Pri rozpade jadra sa teda uvoľní energia
kde W´ = 3Q´2/(20×pi×epsilon0×a´) je energia každého zo vzniknutých nových jadier s polomerom a' s celkovým nábojom Q' (predpokladáme, že nové jadrá sa vzdialia na veľkú vzdialenosť). Možno si položiť otázku, kde sa táto energia v jadre berie. Odpoveď je nasledovná: je to energia jadrových príťažlivých síl, ktorými je jadro držané pokope. Sú to sily krátkeho dosahu, zatiaľ čo elektrické sily sú ďalekého dosahu. Ak by týchto, jadrových síl nebolo, jadro by sa rozletelo účinkom odpudivých síl protónov. Ak je štiepneho materiálu nadkritické množstvo, potom po rozpade prvého jadra napríklad na jadrá brómu a lantánu sa uvoľnia aj ďalšie 3 neutróny, ktoré vyvolajú ďalšie rozpady a vznikne reťazová reakcia.
Nové jadrá po rozpade majú náboje Q ' = Q/2 a polomery a' = a/(21/3). K vypočítaniu energie jadra U235 treba ešte vypočítať polomer pôvodného atómového jadra. Zo známeho celkového náboja jadra U235 Q = 92e a známej objemovej hustoty náboja, plynie pre polomer a hodnota a = (3Q/(4×pi×ro))(1/3) = 6,417.10-15 m a uvoľnená energia každým z pôvodným jadier bude
deltaW = W(1 – 2–2/3) = 6,8.10–11 J = 425 MeV,
kde 1 Mev = 1,602.10-13 J (joule). (Podľa presnejších výpočtov plynúcich z atómovej fyziky uvoľnená energia je cca 200 MeV - pozri napr. Beiser A.: Úvod do moderní fyziky, Academia Praha 1975). Pre rádový odhad uvoľnenej jadrovej energie budeme predpokladať, že kilogram štiepneho materiálu obsahuje
n = 1/(235mp) = 2,55.1024 kg-1
jadier U235. Uvoľnená energia z jedného kilogramu štiepneho materiálu je
Wkg = deltaW×n = 1,73.1014 J.kg-1.
Toto číslo nedáva dobrú predstavu o veľkosti energie, preto sa explozívna energia výbušnín obyčajne udáva v množstve uvoľnenej energie pri výbuchu jednej tonu brizantnej trhaviny – trinitrotoluénu (1 t TNT), pričom 1 t TNT ≈ 4,2.109 J. Uvoľnená jadrová energia na jeden kilogram štiepneho materiálu je teda
W = 1,73.1014 J.kg-1 = 41 254 t TNT.kg-1 ≈ 41 kiloton TNT.kg-1!!!
Pre porovnanie možno ešte uviesť, že táto energia je ekvivalentná tepelnej energii získanej spálením približne 6000 ton kvalitného čierneho uhlia! Na internete sa možno dozvedieť, že v bombe "Little Boy", ktorá zničila Hirošimu sa pri výbuchu z 0,7 kg hmotnosti U235 iba 0,6 g premenilo na energiu podľa vzorca W = mc2. Skutočná uvoľnená energia na kilogram je asi polovica nami získanej hodnoty, čo je tiež dosť.

Hríbovitý mrak atómovej bomby Nagasaki, J aponsko 1945.
Výška asi 18 kilometrov nad hypocentrom
Nuž myslím, že tento výsledok nepotrebuje žiadny komentár. V kilograme látky je ukrytá obrovská energia. Fyzika priniesla ľudstvu veľa dobrého, ale dalo by sa povedať, že vývojom takej hroznej zbrane sa deklasovala do úlohy hrozného zabijaka. Samozrejme, že to je nezmysel, nebola to fyzika, kto uvrhol Hirošimu a Nagasaki do takého hrozného inferna, bol to človek a historické súvislosti. Nemám zďaleka právo hodnotiť morálnu stránku veci, ale nikto nevie povedať koľko miliónov ľudí by ešte bolo prišlo o život, keby sa nebolo stalo to, čo sa stalo. Želám Vám dobrý a pokojný deň! Autor
15.8.2008
14. Ako funguje mikrovlnová rúra – „mikrovlnka“ ?
Väčšina ľudí, ktorí sa pozrú na obr. 1 vedia o čo ide – áno, je to známa mikrovlnová rúra, ktorá dnes už asi nechýba v žiadnej domácnosti. Mikrovlnová rúra sa používa na rýchly a ekonomický ohrev potravín prostredníctvom vody, presnejšie jej molekúl, ktorú potrava vo väčšom, alebo menšom množstve obsahuje. Mikrovlny, ktoré toto ohrievaniu sprostredkujú, sú elektromagnetické vlny s nie celkom presne vymedzeným frekvenčným pásmom. Začínajú pri frekvencii cca 300 MHz = 0,3 GHz (decimetrové vlny) a končia pri 3.105 MHz = 300 GHz (submilimetrové vlny). Ako mnoho iných civilných zariadení, mikrovlnová rúra vznikla ako vedľajší produkt pri vývoji radarovej techniky pre vojenské účely v priebehu druhej svetovej vojny. Jeden vojenský technik pracujúci s magnetrónom si všimol, že čokoláda, ktorú mal vo vrecku, sa mu roztopila.

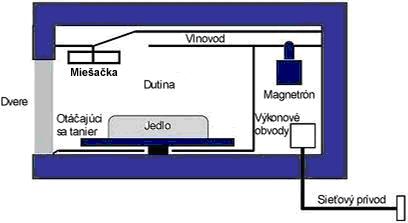
Obr. 1 Obr. 2
Prvá mikrovlnová rúra bola vyrobená v USA v roku 1947. Bolo to 1,8 m vysoké, 340 kg ťažké, vodou chladené monštrum, ktoré spotrebovávalo 3 kW elektrického výkonu. Jeho cena bola 5000 US$.
Srdcom mikrovlnovej rúry je výkonný generátor elektromagnetického výkonu - magnetrón - pracujúci na presne definovanej frekvencii 2,45 GHz = 2,45.109 Hz (odpovedajúcej vlnovej dĺžke 12,24 cm). Táto frekvencia je medzinárodne dohodnutá (pozri nižšie). Činnosti magnetrónu sa budeme venovať v osobitnom odseku nižšie a možno ju nájsť aj v učebnici "Mikrovlnové generátory" na tejto webovej stránke.
Vnútorné usporiadanie mikrovlnovej rúry je na obr. 2. V skrinke s dvojitými kovovými stenami je umiestnený magnetrón s výkonovými obvodmi, vysokonapäťovým transformátorom, s magnetom alebo elektromagnetom a sieťovými filtrami. Magnetrón potrebuje na prevádzku anódové napätie až niekoľko kilovoltov a silné magnetické pole rádovo stovky militesla.
Mikrovlnový elektromagnetický výkon produkovaný magnetrónu sa vlnovodom privádza do dutiny, v ktorej na otáčavom sklenenom tanieri je umiestnená ohrievaná potrava. V závislosti od rozmiestnenia potravy v objeme dutiny môžu v nej vzniknúť stojaté elektromagnetické vlny, otáčavý tanier zaručuje rovnomernejšie ohrievanie. Vo veľkých rúrach k tomuto účelu slúži aj miešačka, ktorá svojimi kovovými lopatkami odráža mikrovlnový výkon a tak ho rozptyľuje do potravy. K vybaveniu skrinky ešte patrí halogénové osvetlenie a ventilátor chladenia magnetrónu. Skrinku uzatvárajú dvierka s okienkom, osadeným dvojitým sklom a husto perforovaným vodivým plechom s otvormi cca 1 mm. Otvory v plechu sú dostatočné malé, aby zabránili úniku elektromagnetickému výkonu von z rúry a dostatočne veľké, aby nimi bolo možno ohrev pozorovať. Dvierka sú opatrene rezonančným elektromagnetickým tesnením, ktoré je bezkontaktné, ďalej pohlcujúcim stratovým tesnením a mechanickým uzáverom, ktorý v prípade náhodného otvorenia počas činnosti rúry okamžite vypne magnetrón. Otázkam bezpečnosti mikrovlnovej rúry je pri jej výrobe venovaná zvlášť veľká pozornosť.
Fyzikálne vlastnosti vody
Aby sme pochopili v čom spočíva elektromagnetický ohrev vody, ktorú obsahuje potrava, treba poznať jej fyzikálne vlastnosti. Voda je silne polárna kvapalina, ktorej molekuly H2O (pozri obr. 3), sú elektrické dipóly s veľkým dipólovým momentom p = 6,14.10-30 C.m, preto je voda aj dobrým rozpúšťadlom rôznych solí (pre porovnanie – molekula jedovatého metylalkoholu CH3OH, väčšia ako H2O, má menší dipólový moment p = 5,67.10-30 C.m, ale je tiež relatívne dobrým rozpúšťadlom). Na molekule H2O si treba všimnúť to, že dva atómy vodíka H sú na atóme kyslíka O naviazané pod stredovým uhlom 105º 3´. Táto konfigurácia atómov nie je vrtochom prírody, je to energeticky najvýhodnejšie zoskupenie atómov v danej molekule, čo však možno dokázať iba prostriedkami kvantovej fyziky. Práve takéto rozmiestenie atómov spôsobuje, že molekula vody je dipólom. (Ak by napr. príslušný uhol bol 180º, ako je to napr. u molekuly oxidu uhličitého CO2, voda by – so všetkými dôsledkami – bola nepolárnou látkou. Nebola by napríklad tým vynikajúcim rozpúšťadlom, akým voda je.). Dipólový moment p je vektor, a na obrázku molekuly vody smeruje od záporného náboja "–" ku kladnému náboju "+".

Obr. 3
Ak sa dipól ocitne v elektrickom polí intenzity E, pole na neho pôsobí točivým momentom p×E a ak je dipól (molekula H2O) voľný, otočí sa do jeho smeru, ak sa smer poľa otočí, otočí sa aj dipól. Ak je pole striedavé, bude dipól vykonávať kmity, alebo rotáciu okolo stredu atómu kyslíka O. Takýto pohyb sa v konečnom dôsledku makroskopicky prejavuje ako teplota. Niekde sa dočítate, že molekuly sa pri svojom pohybe trú o seba a tak vzniká teplo. Molekuly sa nepotrebujú, ani nemôžu trieť, môžu však do seba narážať. Samotný ich pohyb je teplota ako pocitový fenomén. (Neviem si predstaviť ako sa molekula môže s inou molekulou trieť, trieť sa môžu predmety makroskopickej veľkosti). Kmitavý pohyb dipólov sa prenáša aj na nepolárne zložky potravy (dostanú sa tiež do kmitania) a tak ohrievanie je rovnomerné v celom objeme potravy. Na rozdiel od klasického ohrevu, ktorý je povrchový a teplo preniká do hĺbky postupne, pre mikrovlnový ohrev je charakteristické, že elektromagnetická energia vstupuje do vnútra objemu a ohrev je okamžitý a objemový.
Aby k pohybu dipólov došlo, musia byť molekuly, lepšie povedané dipóly, relatívne voľné. Ak sa voda nachádza v stave vodných pár, absorpcia elektromagnetickej energie je najľahšia, relatívne ľahká je aj v kvapalnej vode, ak je voda zmrznutá, absorpcia mikrovĺn je obmedzená, pretože molekuly sú relatívne silne viazané v kryštalickej mriežke ľadu. Nádoby, v ktorých sa potrava ohrieva neobsahujú dipóly, preto sa mikrovlnovým žiarením priamo neohrievajú a preberajú teplo iba od ohriatej potravy. (Treba dávať pozor napríklad pri ohrievaní kojeneckých fliaš, ktoré na dotyk môžu byť chladné, ale ich obsah pritom vriaci!)
Mikrovlnový spôsob ohrevu sa niekedy nazýva dielektrickým ohrevom, pri ktorom absorbovaný elektromagnetický výkon je úmerný kvadrátu amplitúdy elektrického poľa a imaginárnej časti komplexnej permitivity materiálu, nenastáva však ako rezonančná absorpcia, ako sa to niekedy tvrdí. Voda má svoju najnižšiu rezonančnú frekvencii pri 18 GHz a molekuly vodných pár majú rezonanciu pri frekvencii 22,23508 GHz. Pri takých vysokých frekvenciách by bol ohrev veľmi neekonomický a drahý. Frekvencia 2,45 GHz bola zvolená ako výsledok radu kompromisov:
-
Výkonný generátor – magnetrón s minimálne 500 W výkonu musí byť jednoduchý a spoľahlivý, s nízkymi nákladmi na výrobu.
-
Vlnová dĺžka (12,24 cm) musí byť podstatne menšia ako rozmery ohrievaného priestoru.
-
Vlnová dĺžka (frekvencia) musí zostať nemenná, inač rezonančné bezkontaktné tesnenie dverí bude neúčinné.
-
V rezervovanom frekvenčného pásma ISM (industrial, scientific and medical radio band 2,4 – 2,5 GHz) nesmú pracovať žiadne telekomunikačné služby.
-
Hĺbka prieniku elektromagnetických vĺn (v dôsledku skinefektu) do ohrievanej potravy musí byť dostačujúca. Čím nižšia je frekvencia, tým väčšia je hĺbka prieniku, ale aj absorpcia elektromagnetických vĺn je horšia. Naopak čím vyššia je frekvencia tým menšia je hĺbka prieniku, čo znamená, že ohrev je povrchový. Pri frekvencii 2,45 GHz prienik elektromagnetických vĺn do ohrievanej masy je niekoľko centimetrov. Okrem uvedenej frekvencie existuje ešte niekoľko ISM frekvenčných pásiem, pri ktorých je ohrev možný, tie sa však málo využívajú.
Magnetrón
Prvý magnetrón bol vyrobený v USA počas druhej svetovej vojny na radarové účely. Je to výkonný generátor elektromagnetických kmitov, ktorého činnosť sa zakladá na špecifickej interakcii zväzku elektrónov so skríženým elektrickým a magnetickým poľom. Z rozličných typov vyvinutých magnetrónov praktické uplatnenie v mikrovlnových rúrach, dosiahol mnohodutinový magnetrón, ktorý je v reze, bez magnetu a chladiacich rebier, znázornený na obr. 4. Jeho podstatnou časťou je masívny anódový blok (pozri tiež obr. 5 a 6a) s vyfrézovanými rovnakými rezonančnými dutinami (rezonátory), z ktorých jedna je zobrazená na obr. 6b. Tento blok je dopadom elektrónov silne ohrievaný a musí sa chladiť rebrami na bloku a ventilátorom. Počet rezonátorov bloku je rôzny (zvyčajne 8), musí však byť párny. Každý rezonátor možno považovať za paralelný rezonančný LC obvod, ktorého indukčnosť je tvorená valcovou plochou a kapacitu predstavujú paralelné rovinné plochy (štrbiny) na ústi valcov (na obr. 6b), alebo hrany valcových plôch (na obr. 5). Rezonančná frekvencia rezonátorov je v prvom priblížení frekvenciou, na ktorej magnetrón kmitá, pričom počet dutín len málo ovplyvňuje výslednú frekvenciu. Axiálne, vo vnútri bloku, je uložená katóda s vysokou emisnou schopnosťou (obr. 6a).
Elektróny emitované katódou sa pohybujú pod účinkom radiálneho elektrického poľa medzi katódou a anódou a statického magnetického poľa, ktoré má smer osi katódy. V priestore interakcie – medzi katódou a anódou – sa elektróny pohybujú po zložitých dráhach, ktoré sú superpozíciou špirál a cykloíd a za istých predpokladov sú schopné odovzdávať svoju kinetickú energiu vysokofrekvenčnému elektromagnetickému poľu rezonátorov, čím sa v magnetróne udržiavajú výkonné netlmené elektromagnetické kmity.
Napriek tomu, že sa dnes magnetróny široko používajú, exaktná analýza ich činnosti ani dodnes neexistuje. Príčinou je zložitá interakcia elektromagnetického poľa s elektrónmi, ktorá má za následok niekoľko možných typov (módov) vybudenia kmitov, ďalej je to značný vplyv objemového elektrického náboja v interakčnom priestore a geometrická zložitosť interakčného priestoru.

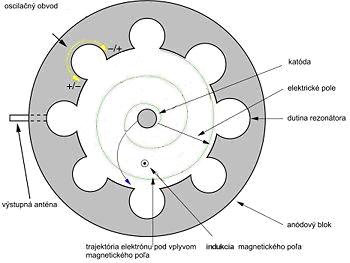
Obr. 4 Obr. 5
Bez prítomnosti magnetického poľa uvoľnené elektróny emitované katódou by radiálne dopadali na anódu, a magnetrón by pracoval ako obyčajná vákuová dióda. Situácia sa radikálne zmení, ak v magnetróne pôsobí magnetické pole v smere pozdĺž osi katódy. Pod účinkom magnetického poľa sa radiálne dráhy elektrónov začnú zakrivovať a zmenia sa na špirály (zelená špirála na obr. 5). Elektróny pohybujúce sa popred ústia rezonátorov na obr. 5 svojím induktívnym účinkom vybudia v stenách rezonátoroch prúdy (zobrazené žlto) a následne v rezonátoroch prahové elektromagnetické kmity, ktorých elektrická zložka je najsilnejšia v kapacitných štrbinách (obr. 6a,b), alebo na hranách rezonátorov (medzi špičkami žltých šipiek +/- a -/+ na obr. 5). Toto pole vystupuje aj do vnútornej interakčnej dutiny magnetrónu okolo katódy. Dráha elektrónov sa skomplikuje, pretože na ňu bude pôsobiť aj vysokofrekvenčné polia štrbín, čo má za následok, že na špirálu bude ešte superponovaný cykloidálny pohyb. Podrobnú teóriu činnosti mnohodutinového magnetrónu možno nájsť napr. v učebnici "Mikrovlnové generátory", uloženej na tejto webovej stránke.
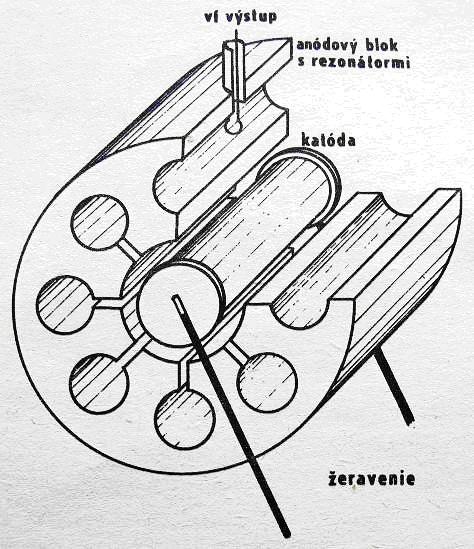
 Obr. 6a Obr. 6b
Obr. 6a Obr. 6b
Aby magnetrón trvalo kmital, musia elektróny letiace popred štrbiny trvalo odovzdávať svoju kinetickú energiu elektrickému poľu rezonátorov, t.j. v tomto poli elektróny musia byť brzdené. Mrak brzdených a niektorých urýchľovaných elektrónov v interakčnom priestore má v tejto situácii samofokusačný účinok a z elektrónového mraku sa vyformujú „špice“ imaginárneho kolesa (4 špice v 8-rezonátorovom magnetróne), „koleso“ sa otáča a prechodom elektrónových "špíc" popred štrbiny rezonátorov elektróny odovzdávajú rezonátorom svoju kinetickú energiu na zvýšenie energie elektromagnetického poľa. Takúto situáciu možno dosiahnuť vhodným nastavením anódového napätia a magnetickej indukcie. Samozrejme, že v mikrovlnovej rúre v domácnosti sa nič nenastavuje, tieto parametre sú nastavené výrobcom. Vidíme, že činnosť magnetrónu je veľmi zložitá a delikátna – napriek tomu magnetróny spoľahlivo, s veľkým výkonom pracujú. V mikrovlnových rúrach určených pre domácnosti pracujú s mikrovlnovým výkonom od 500 W do cca 1500 W s účinnosťou cca 50%, teda s príkonom od 1000 W do cca 3000 W. Je to vysoký výkon, ale netreba zabúdať, že v jednom cykle, pri jednom ohreve jedla, magnetron pracuje iba pár minút, tak že odobraná elektrická energia je veľmi malá, pritom všetka vysokofrekvenčná energia sa spotrebuje len na ohrev potravy. Zvyšok elektrického príkonu sa mení na teplo magnetrónu a ostatných elektrických súčiastok, pričom aj toto teplo sa ventilátorom vháňa do priestoru, kde sa potrava ohrieva.
*****
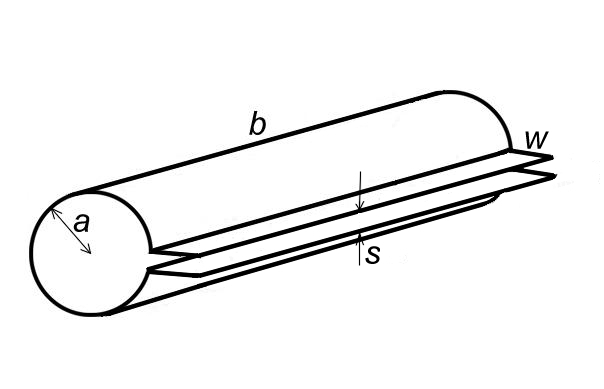
Nakoniec bude zaujímavé numerickým výpočtom odhadnúť frekvenciu, na ktorej magnetrón kmitá. Budeme predpokladať, že rezonátory magnetrónu majú dobre definovanú kapacitnú a induktívnu časť, čím bude možne na výpočet frekvencie využiť známy Thomsonov vzorec. Takým magnetrónom je napríklad magnetrón na obr. 6a. Polomer valcových induktívnych časti je a (pozri obr. 6b), kapacitné plôšky sú rozmerov w × b a vzdialenosť plošiek je s. Platí, že b » a a s « w.
Magnetrón, s parametrami: a = 6,8 mm, s = 1 mm, w = 8,2 mm vyhovuje pre použitie v mikrovlnovej rúre. Vypočítame číselne rezonančnú frekvenciu a vlnovú dĺžku kmitov takého magnetrónu. V dutine je voľný priestor (vákuum).
Predpokladajme, že magnetrón kmitá, t. j. po vnútornej valcovej ploche rezonátora tečie solenoidálne striedavý prúd s amplitúdou plošnej prúdovej hustoty Js (žltá časť kružnice - pozri obr. 5). Vo vnútri valca vytvorí tento prúd osové magnetické pole s amplitúdou indukcie B = µ0Js, µ0 je magnetická konštanta (permeabilita voľného priestoru). Amplitúda indukčného toku Fi v smere osi valca, jeho prierezom, je (aj tu musíme niektoré grécke písmená vypisovať latinkou)
Fi = LI = piµ0a2Js = (piµ0a2/b)I,
kde L je indukčnosť valcovej plochy a I = bJs je amplitúda celkového prúdu tečúceho po vnútornom povrchu valca, pi = 3,14159..... je Ludolfovo číslo („žltý“ prúd po vnútornom povrchu valca na obr. 5 – takýto valec je vlastne solenoid s jedným, širokým závitom). Pre indukčnosť valca plynie
L = piµ0a2/b.
Kapacita rovinných plôch je
C = epsilon0wb/s,
(epsilon0 je elektrická konštanta - permitivita voľného priestoru), takže rezonančná frekvencia
frez = 1/(2pi(LC)(1/2) ) = (c/(2pia))(s/w)(1/2),
kde c = 1/(epsilon0µ0)(1/2) = 299 792 458 m/s je rýchlosť svetla. Po dosadení numerických parametrov magnetrónu dostaneme rezonančnú frekvenciu magnetrónu
frez = 2 450,3 MHz = 2,4503 GHz,
alebo rezonančnú vlnovú dĺžku
lambdarez = c /frez = 12,24 cm.
Číselný výsledok nám poskytuje predstavu o tom, aké musia byť vnútorné parametre magnetrónu, ak jeho rezonančná frekvencia, resp. rezonančná vlnová dĺžka majú spĺňať požiadavky ISM. Želám Vám pekný a príjemný deň! Autor
31.8.2008
15. Fyzikálne úlohy a ich postavenie pri štúdiu fyziky.
Úspešné a kvalitné štúdium fyziky pozostáva z troch časti: a) z dokonalej teoretickej prípravy z predmetu, počúvaním kvalitných prednášok podporovaných samoštúdiom, b) z absolvovania vhodne vybraného súboru kvalitných praktických úloh (praktiká) a c) z riešenia výpočtových fyzikálnych úloh. Zatiaľ čo prvé dve časti sú v značnej miere závisle od kvalitných učiteľov, učebníc a dobre zariadených laboratórií, riešenie fyzikálnych úloh je záležitosť, ktorá je plne v kompetencii samotného študenta. Vo všeobecnosti možno povedať, že fyziku ovláda ten, kto vie riešiť fyzikálne úlohy, a experimentálny fyzik musí mať aj primeranú zručnosť a tvorivosť.
Najväčší problém pri riešení fyzikálnej úlohy je obvykle odpoveď na otázku: "Ako začať?" Niet na ňu jednoznačnej odpovede. Predpokladom úspešného riešenia úloh je dokonale ovládanie fyzikálnej problematiky, s ktorou úloha súvisí. Úspech sa dostaví až po tvrdej a systematickej práci s úlohami a získaním dostatočnej skúsenosti. Ako pri skutočnom fyzikálnom výskume, ani pri riešení úlohy, nie je vždy od začiatku jasné, aká je optimálna postupnosť krokov pre dosiahnutie výsledku. Ak možno niečo poradiť – tak potom popri špeciálnych zákonoch týkajúcich sa priamo zadanej fyzikálnej úlohy, treba sa pri jej riešení pokúsiť využiť fundamentálne fyzikálne zákony, ako sú napr. zákony zachovania a princíp superpozície. Ešte vyšší stupeň chápania problému predpokladá schopnosť využívania metodologických princípov fyziky, ako sú: princíp príčinnosti, symetrie, relativity a ekvivalencie. Niekedy sa treba tiež povzniesť nad priehradky, ktoré sme vo fyzike narobili. Fyzikálny svet je zložitý a mnohotvárny a často sa treba na problém vedieť pozrieť aj z inej, nielen "elektromagnetickej", ale napr. aj z mechanickej, či termodynamickej stránky.
Umenie riešenia fyzikálnych úloh spočíva tiež v schopnosti odlíšiť podstatné stránky problému od menej podstatných, či nepodstatných. Takáto schopnosť sa pri riešení prejaví schopnosťou zanedbávať tak, že sa výpočty stanú matematicky jednoduchšie, pričom výsledok riešenia problému zostáva pre prax dostatočne presný. Dobrým príkladom je zanedbanie gravitačného pôsobenia pri elektromagnetickej interakcii elementárnych častíc, kde odstup silového pôsobenia je až 39 rádov (elektrická sila je ~1039-krát väčšia ako gravitačná - pozri „Elektromagnetizmus“, kap. 1).
Pri teoretických úlohách výsledkom riešenia je nejaký vzťah, alebo dôkaz nejakého tvrdenia, u praktických úloh sa najčastejšie vyžaduje numerický výsledok. Numerická úloha má poukázať na konkrétne kvantitatívne súvislosti, ktoré môžu byť pre budúceho profesionálneho fyzika veľmi poučné. Veď dozvedieť sa numerickým výpočtom napr. to, že vo vnútri vodíkového atómu je intenzita elektrického poľa väčšia ako 1012 V/m a rastie smerom do vnútra k neznámym hodnotám, že magnetická indukcia v strede atómu dosahuje tiež extrémne vysokých hodnôt cca 12 T, je poznanie veľmi vzrušujúce a šokujúce zároveň (pozri v učebnici „Elektromagnetizmus“, úlohy 9 a 170). Atóm takto predstavuje singularitu hustoty elektromagnetickej energie.
V dnešnej dobe pri súčasných možnostiach výpočtovej techniky ani zložité numerické výpočty pri riešení úloh nepredstavujú nijaké mimoriadne problémy. Dnes nerobia problémy ani úlohy napríklad s eliptickými integrálmi, alebo s Besselovymi, prípadne inými špeciálnymi funkciami, ktorých hodnoty voľakedy bolo treba hľadať v špeciálnych tabuľkách, dnes s vysokou presnosťou umožňujú vypočítať rôzne počítačové programy a tak matematické tabuľky sa stávajú zbytočné. Mnohé úlohy v učebnici „Elektromagnetizmus“ autor numericky riešil v čase, keď mal k dispozícii ako jedinú výpočtovú techniku logaritmické pravítko, k tomu matematicko-fyzikálne tabuľky, papier a ceruzku.
Všetky úlohy v učebniciach uvedených na tejto webovej stránke majú pripojené aj riešenia. Riešená zbierka úloh má svoje výhody, ale aj nevýhody. Výhodou je, že zbavuje študenta pochybností pri hodnotení svojho riešenia, nevýhodou je, že zvádza na "odpisovanie". Fyzikálne úlohy majú predovšetkým preveriť hĺbku a rozsah teoretickej prípravy študenta a jeho schopnosť samostatne riešiť úlohy fyzikálnej praxe. Mali by byť preto riešené samostatne, bez pomoci nejakých vzorových riešení, ak naviac uvážime, že úlohy môžu mať niekoľko správnych spôsobov riešenia, obvykle však iba s jedným správnym výsledkom. Študent by po riešeniach mal siahnuť iba pri konfrontácii vlastného postupu a dosiahnutého riešenia. Ak si musí nimi pomáhať pred dosiahnutím vlastného výsledku, znamená to, že jeho príprava nebola dostatočná, alebo nemá dostatok trpezlivosti. Riešenia sú aj v takom prípade užitočné, ale iba ako dodatočná študijná literatúra. Mnohé fyzikálne učebnice s úlohami, hlavne v USA, sa vydávajú bez riešení. Autori tieto riešenia vydávajú ako zvláštne príručky, ktoré si študent môže zakúpiť (nakoniec autor má právo na odmenu za nezanedbateľnú prácu pri riešení úloh).
Napriek argumentom pre a proti si myslím, že riešené úlohy môžu byť užitočnou pomôckou, ak sa riešenia používajú v rozumnej miere. Želám Vám veľa úspechov pri riešení fyzikálnych úloh a veľa nových poznatkov v novom školskom roku! Autor
11.9.2008

