Elektromagnetické javy a ich miesto v elektronike

úvaha 31-35 |
 |
|
OBSAH:
31. Oliver Heaviside – priekopník vektorového počtu 32. Symbolicko-komplexný počet – záchranca striedavých elektrických sieti
33. Čo je to neper (Np), bel (B), alebo decibel (dB, dBm, dBW)?
34. James Clerk Maxwell
35. Vychádza monografia „Elektromagnetizmus“ !!!
___________________________________________________________________________
31. Oliver Heaviside – priekopník vektorového počtu
Mám odmietnuť chutné jedlo len preto,
že nerozumiem zažívacím procesom?
Oliver Heaviside
Oliver Heaviside (18. mája 1850 – 3. februára 1925) bol anglický samouk, napriek tomu bol považovaný za elektrotechnického inžiniera, matematika a fyzika. Bol súčasníkom Hermanna von Helmholtza, Heinricha Hertza a Lorda Rayleigha. Teoretickí fyzici meno Oliver Heaviside takmer nespomínajú, hoci bol to on, kto prvý raz napísal štyri Maxwellové rovnice vo vektorovom tvare, tak ako ich dnes poznáme a ako ich nikto predtým nevidel. Keď Ludwig Boltzmann prvýraz uvidel vektorový zápis Maxwellovych rovníc, ako vo vytržení zvolal, „bol to snáď Boh, čo písal tieto riadky ...?“ („War es ein Gott, der diese Zeilen schrieb ...?“, 1893). V pôvodnom ťažkopádnom Maxwellovom spise sa tieto rovnice takmer strácajú, preto považujem Heavisideovu zásluhu o rovnice za porovnateľnú s Maxwellovou. Možno že Heavisidea nespomínajú aj preto, že bol iba samouk.
Hneď na úvod treba povedať, že okrem reformulácií Maxwellových rovníc je Heaviside autorom operátorového počtu, pôvodca symbolicko-komplexnej metódy analýzy harmonických striedavých elektrických obvodov a sieti, bez ktorej by si dnes elektrotechnickí inžinieri nevedeli poradiť. Má veľký podiel na vzniku teórie dlhých dvojvodičových prenosových vedení a na formulácii telegrafných rovníc, zaviedol takmer všetky pojmy v teórii striedavých elektrických prúdov a v teórii elektromagnetických vĺn. Hoci musel celý život bojovať so zaužívanými škrupulóznymi vedeckými zvyklosťami, Heaviside zmenil tvár aplikovanej matematiky a fyziky do podoby, v ktorej ich poznáme dnes. Už len pre tieto jeho zásluhy Heaviside patri do galérie najväčších osobností fyziky a elektrotechniky a v neposlednom rade aj matematiky.
 
Oliver Heaviside Heavisideov hrob
(1850 – 1925) na Paingntonskom cintorine
Narodil sa v Londýnskom Camden Town. Bol malý a ryšavý, v mladosti ochorel na šarlach, takže čiastočne ohluchol a v starobe bol úplne hluchý. V škole bol výborným žiakom, v hodnotení v roku 1865 bol piaty z päťsto žiakov. Heavisideov strýko, Sir Charles Wheatstone (1802–1875) v roku 1830 spoluvynáliezol telegraf, čo mu prinieslo slávu a uznanie ako experta v telegrafii a v elektromagnetizme. Sestra Heavisideovej matky bola manželkou Sira Wheatstonea, ktorý sa intenzívne zaujímal o chlapcovo vzdelávanie.
V šestnástich rokoch Heaviside zanechal školu a vzdelával sa sám doma v telegrafii a v elektromagnetizme. Doma študoval „na plný úväzok“, do svojich osemnástich rokov. Potom prijal zamestnanie – jediné platené v jeho živote – ako telegrafný operátor v spoločnosti Great Northern Telegraph Company najprv v Dánsku, neskôr v Newcastle-upon-Tyne, kde sa čoskoro stal šéfoperátorom. Popri práci ďalej študoval a žil s rodičmi v ich dome. Celý život sa neoženil.
V roku 1873 vyšla kniha Jamesa Clerka Maxwella „Treatise on Electricity and Magnetism“ (Pojednanie o elektrine a magnetizme), ktorá Heavisidea veľmi zaujala. Neskôr spomína:
Moje prvé stretnutie s veľkým Maxwellovym „pojednaním“ sa udialo, keď som bol ešte mladý muž. Hneď som videl, aké obrovské možnosti poskytuje táto kniha pre aplikácie. Bol som rozhodnutý ju zvládnuť a pustil som sa do nej hneď, ale správal som sa ako vyslovený ignorant. Veľmi rýchle som zistil, že nemám potrebné znalosti z matematickej analýzy (v škole som sa učil iba algebru a trigonometriu, ktoré som pomaly aj zabudol) a tak moja práca skončila skôr ako začala. Prešlo viac rokov než som sa k nej mohol vrátiť. Zatiaľ som Maxwella odložil a pustil som sa svojou vlastnou cestou. A postupoval som oveľa rýchlejšie ... Samo sebou sa rozumie, že som hlásal a presadzoval moju interpretáciu Maxwella.
V roku 1880 sa Heaviside zaoberal skinefektom na telegrafných vedeniach a v tom istom roku patentoval koaxiálne vedenie (koaxiálny kábel). V tom čase rozvíjať teóriu prenosových vedení, ktorej základ tvoria telegrafné rovnice (pozri napr. „Elektronika veľmi vysokých frekvencií“, kap. 6, odsek 1, na tejto webovej stránke). Jeho teoretické práce značne prispeli k rozvoju praktickej telegrafie.
V roku 1887 sa zaoberal známym problémom elektrotechnikov, že totiž pre praktické účely prirodzená vlnová impedancia koaxiálneho kábla (L/C)1/2 je nízka, čo vedie k skresľovaniu signálov a preto ju treba umelo zvyšovať tým, že sa zvyšuje pozdĺžnu indukčnosť kábla, robí sa to známou „pupináciou“ – elektroinžinierom, ktorí pracujú v oblasti prenosových vedení, tento pojem niečo hovorí. O prvenstvo pri riešení tejto problematiky obrala Heavisida spoločnosť AT&T, ktorá si na riešenie problému najala dvoch vedcov Georgea A. Campbella a Michaela I. Pupina. Tí rozvinuli Heavisideove myšlienky a spoločnosť získala patent na riešenie problému. Zisky z patentu plne pokryli ich výdaje na výskum a technické zabezpečenie výroby cievok, ktoré vymyslel Heaviside. Spoločnosť ponúkla Heavisideovi finančné odškodnenie, ktoré však on neprijal a žiadal o podiel na patente. Heaviside bol chronicky chudobný a toto gesto iba zvýšilo jeho biedu.
Snáď najväčšia zásluha Heavisidea je v tom, že v roku 1884 pretvoril Maxwellovu teóriu elektromagnetického poľa z jej pôvodnej ťažkopádnej zložkovej podoby 20 rovníc pre 20 premenných na štyri vektorové rovnice, pre štyri vektory (E, B, D, H) dané prúdovými J a nábojovými ro hustotami, pričom využil operátory rotácie (rot, alebo angl. curl) a divergencie (div) z vektorového počtu. Štyri vektorové diferenciálne rovnice sú dnes všeobecne známe ako Maxwellove rovnice a opisujú elektromagnetické javy vznikajúce v celom frekvenčnom pásme od nulovej až po optické frekvencie (pozri napr. „Elektromagnetizmus“, kap. 8, ods. 7, tu).
Medzi rokmi 1880 až 1887 Heaviside pracoval na vektorovom a operátorovom počte, v ktorom zaviedol označenie D pre diferenciálny operátor. Operátorový počet je metóda na riešenie diferenciálnych rovníc ich transformáciou na algebrické. Metóda po jej zverejnení vyvolala značnú kontraverziu pre nedostatok rigoróznosti pri jej odvádzaní. Pri tej príležitosti Heaviside povedal známy výrok „Matematika je experimentálna veda – prvé je jej využitie a až potom prídu definicie!“ Bola to odpoveď na kritiku, že jeho použitie operátorov je dosť nejasné. Pri ďalšej príležitosti trochu defenzívne konštatoval, že „neodmietne chutné jedlo len preto, že nerozumie zažívacím procesom“. Britský matematik Thomas John I´Anson Bromwich neskôr rigoróznym matematickým dôkazom potvrdil Heavisideovu operátorovú metódu. Operátorová metóda je zovšeobecnením vyššie spomínanej symbolicko-komplexná metóda analýzy elektrických obvodov a sieti s harmonickými striedavými prúdmi, ktorú Heaviside formuloval už v roku 1874, teda asi 15 rov skôr, ako sa striedavé prúdy začali v elektrotechnike používať. Prakticky sa metóda začala používať po roku 1893 (pozri „Elektromagnetizmus“, kap. 9, ods. 4, tu).
Z ďalších Heavisideovych prínosov je hodné spomenúť, že do teoretickej elektrotechniky zaviedol skokovú funkciu a použil ju k modelovaniu prúdu v elektrických obvodoch. Nezávisle od iných, Heaviside zaviedol aj Poyntingov vektor (pozri napr. „Elektromagnetizmus“, kap. 11, odsek 4, tiež tu) a názvy prakticky všetkých veličín vystupujúcich v teórii harmonických striedavých prúdov a elektromagnetických vĺn (pozri „Elektromagnetizmus“, str. 446, tu). Sú to napríklad názvy: impedancia, admitancia, reaktancia, susceptancia a mnoho iných.
V dvoch prácach z rokov 1888 a 1889 Heaviside vypočítal deformáciu elektrického a magnetického poľa v okolí pohybujúceho sa náboja, ako aj javy, ktoré vznikajú ak náboj vstúpi do hustého média. Javy, ktoré Heaviside analyzuje predchádzajú to, čo dnes poznáme ako Čerenkovov jav. Priateľa Georga FizGeralda jeho práce inšpirovali k vysloveniu hypotézy o kontrakcii dĺžok v špeciálnej teórii relativity, ktorá sa dnes nazýva Lorentzova-FitzGeraldova kontrakcia (pozri "Elektromagnetizmus", kap. 6, ods 5, tu).
Heaviside prišiel s myšlienkou, že Zem nad atmosférou obklopuje ionizovaná vrstva, ktorá sa nazýva iónosféra. V roku 1902 predpovedal existenciu vodivej Kennelly-Heavisideovej vrstvy v iónosfére, ktorá nesie aj jeho meno. Existencia iónosféry bola dokázaná v roku 1923. Heavisideove predpovede a Planckov vyžarovací zákon odradili vedcov od pokusov prijímať elektromagnetické signály zo slnka a z iných astronomických objektov. V tejto súvislosti Heaviside navrhol spôsob, ako možno vysielať rádiový signál tak, aby kopíroval zakrivenie zemského povrchu odrazom signálov od iónosféry. Nech už sú dôvody akékoľvek, zdá sa, že nasledujúcich 30 rokov sa nikto nepokúšal o príjem elektromagnetických signálov zpoza ionosféry, až do roku 1932, keď vznikla rádioastronómiu.
V roku 1891 britská Kráľovská spoločnosť (British Royal Society) vybrala Heavisidea za člena spoločnosti, za jeho prínos k matematickému opisu elektromagnetických javov. V roku 1905 Univerzita v Göttingene udelila Heavisideovi akademický titul „doctor honoris causa“. V roku 1922 mu ako prvému bola udelená prestížna Faradayova Medaila, ktorá bola práve v tom roku ustanovená. Väčšina ďalších ocenení mu však bola udelená až posmrtne.
V posledných rokoch svojho života sa Heaviside stal excentrickým. Hoci v mladosti aktívne bicykloval, jeho zdravie v šesťdesiatych rokoch života začalo chátrať. Oliver Heaviside zomrel v Torquay v Devone a je pochovaný na Paigntonskom cintoríne. Všetkých Vás srdečne pozdravujem! Autor
14.01.2010
(Životopisné údaje prevzaté z Wikipedie).
32. Symbolicko-komplexný počet
– záchranca analýzy striedavých elektrických sieti
Znovu sa ospravedlňujem čitateľom za používanú nezvyčajnú symboliku striedavých prúdov, ale tento server nemá ani grécke písmená, ani "equations editor" na tvorbu vzorcov (w = omega, fi = fázový uhol, pi = Ludolfovo číslo = 3,14159....).
Pri analýze jednosmerných elektrických sieti je základnou úlohou, pri zadaných elektromotorických napätiach zdrojov a známych odporoch (včítane vnútorných odporoch zdrojov) v sieti nájsť prúdy v jednotlivých odporoch a prípadne napätia na týchto odporoch. Vo väčšine prípadov treba tu riešiť systém algebrických rovníc.
Podobná analýza sa robí na striedavých sieťach, z tým rozdielom, že je zložitejšia. Striedavé elektrické siete, pozostávajú z odporov, kapacít, indukčností, prípadne aj vzájomných indukčností a pôsobia v nich zdroje striedavých elektromotorických napätí s danými amplitúdami a prípadnými fázovými posuvmi (ak treba) oproti referenčnému priebehu rovnakej frekvencie. Neznámymi sú amplitúdy prúdov a ich fázové posuvy v jednotlivých vetvách siete oproti referenčnému striedavému priebehu. Ak v obvode pôsobí len jeden zdroj napätia, možno ho považovať za referenčný a brať jeho fázový posuv za nulový. Príklad jednoduchej striedavej siete je na obr. 1.
Obr. 1
Pri priamočiarom riešení takejto úlohy sa využívajú známe zákony z elektromagnetizmu ako je Ohmov zákon, zákon elektromagnetickej indukcie a zovšeobecnené Kirchhoffove zákony o nulovom súčte napätí v uzavretom elektrickom obvode a nulovým súčte prúdov vtekajúcich, resp. vytekajúcich z uzla. Ak označíme harmonický prúd v nejakom prvku i = i(t), potom napätie na odpore R je uR = Ri, na indukčnosti následne vznikne indukované protinapätie uL = –Ldi/dt a na kapacite C (kondenzátore) je napätie uC = ∫idt/C. Ak okamžité napätie zdroja je u(t), potom súčet všetkých okamžitých potenciálnych spádov (teda napätí na prvkoch, samozrejme s ohľadom na znamienka napätí) v uzavretej slučke siete sa rovná súčtu elektromotorických napätí zdrojov v obvode. Zákon o nulovom celkovom prúde v uzle však platí iba pre kvazistacionárne prúdy, teda také, ktoré sa s časom nemenia príliš rýchle. Rovnice pre jednu slučku a jeden uzol siete majú tvar
uR + uL + uC = u, i1 + i2 + ... + in = 0.
Počet napäťových rovníc sa rovná počtu nezávislých slučiek a počet prúdových rovníc počtu nezávislých uzlov v sieti. Počet vybraných rovníc sa rovná počtu neznámych prúdov (pozri napr. „Elektromagnetizmus“, kap. 5, ods.7).
Ak do vyššie napísaných rovníc dosadíme vyjadrenia napätí, cez jednotlivé prúdy, dostaneme sústavu integrálno-diferenciálnych rovníc pre prúdy v jednotlivých prvkoch. Riešenia sústavy sú superpozíciou nesta-cionárnych (obyčajne exponenciálnych narastajúcich, alebo klesajúcich) prúdov a stacionárnych harmonických (sínusových, alebo kosínusových) prúdov. Nestacionárne, alebo prechodové prúdy po istom čase z riešenia vymiznú a nie sú vždy predmetom záujmu. Zaujímavé sú stacionárne prúdy, ktoré pri harmonickom napäťovom budení
ui(t) = Ui cos wt
budú mať tiež harmonický tvar
ii(t) = Ii cos (wt + fii)
(Ui sú dané amplitúdy napätí, Ii očakávané amplitúdy prúdov, w = 2pif daná kruhová frekvencia, alebo uhlová rýchlosť v rad/s, f je frekvencia v Hz a fii sú fázové posuvy prúdov, i = 1, 2 3, ... n, n je počet hľadaných prúdov). Takéto očakávané riešenie možno dosadiť do systému integrálno-diferenciálnych rovníc, čím tieto prejdú na systém algebrických transcendentných rovníc pre amplitúdy prúdov Ii a ich fázové posuvy fii. Pre jednoduchý sériový RLC obvod je priamy výpočet urobený v učebnici „Elektromagnetizmus“, kap. 9, ods. 2.2.
*****
Aj pre nie príliš zložité elektrické siete s harmonickými striedavými prúdmi je priama analýza s využitím trigonometrických funkcií veľmi nepraktická a ťažkopádna, pretože vedie k veľmi komplikovaným a neprehľadným výrazom prekypujúcich sínusmi a kosínusmi a ich kombináciami. Tieto nedostatky odstraňuje elegantná symbolicko-komplexná metóda, ktorej prednosť je hlavne v tom, že všetky výpočty redukuje z diferenciálnych operácií na algebrické, s komplexnými číslami. V ďalšom budem predpokladať, že čitateľ pozná komplexné čísla a vie s nimi aspoň na elementárnej úrovni narábať a počítať. Ak nie, môže mu v tom veľmi pomôcť tabuľka 16 v citovanej učebnici.
V jednoduchom sériovom RLC obvode napájanom zo zdroja striedavého napätia s amplitúdou U0 pri kruhovej frekvencii w sú amplitúda prúdu I0 a fázový posuv fi dané výrazmi
I0 = U0/{R2 + [wL –1/(wC)]2}1/2 = U0/Z,
fi = arctg{[wL –1/(wC)]/R},
pozri už spomínaný ods. 9.2.2 citovanej učebnice. Veličiny wL a 1/(wC) sú induktívna reaktancia (induktancia) a kapacitná reaktancia (kapacitancia) a majú rozmer odporu. Veličina
Z = U0/I0 = {R2 + [wL –1/(wC)]2}1/2
sa nazýva impedancia (tak ju nazval Oliver Heaviside – pozri úvahu 31) a je daná pomerom amplitúdy napätia na trojici prvkov RLC a amplitúdy prúdu, ktorý tečie v obvode zdroja. Zdroje striedavých napätí obyčajne majú aj nejakú vnútornú impedanciu, ktorá sa prejavuje na ich výstupných svorkách. V najjednoduchších prípadoch sa tieto impedancie redukujú na ich vnútorné odpory a to treba pri analýze sieti tiež brať do úvahy.
Anglický fyzik a elektrotechnik Oliver Heaviside (1850 –1925) si všimol, že amplitúdu a fázový posuv prúdu možno zlúčiť do jednej informácie a vytvoriť komplexné číslo
I0 = U0/Z = (U0/Z2)Z*,
ktoré Heaviside nazval komplexný prúd (obraz) a veličinu
Z = U0/I0 = R + j [wL –1/(wC)]
nazval komplexnou impedanciou RLC vetvy. Matematická veličina j sa nazýva imaginárna jednotka, pre ktorú platí: j2 = –1. Veličina Z* je komplexne združená impedancia k Z, pričom platí: ZZ* = |Z|2 = Z2. S takto skonštruovaným komplexným obrazom prúdu možno pracovať ako s reálnym prúdom, pričom po skončení všetkých výpočtových operácii skutočný prúd (amplitúda a fázový posuv) bude reálnou alebo imaginárnou časťou komplexného výsledku.
Symbolická-komplexná metóda spočíva na jednoduchých myšlienkach, ktoré možno sformulovať takto: Striedavý prúd i = I0 cos(wt + fi), alebo i = I0 sin(wt + fi), možno pre účely analýzy nahradiť komplexným číslom (obrazom) i = I0cos(wt + fi) + jI0sin(wt + fi) = I0ej(wt + fi) = (I0ejfi)ejwt = I0ejwt t. j. číslom, ktorého reálna časť je I0 cos(wt + fi)
a imaginárna časť
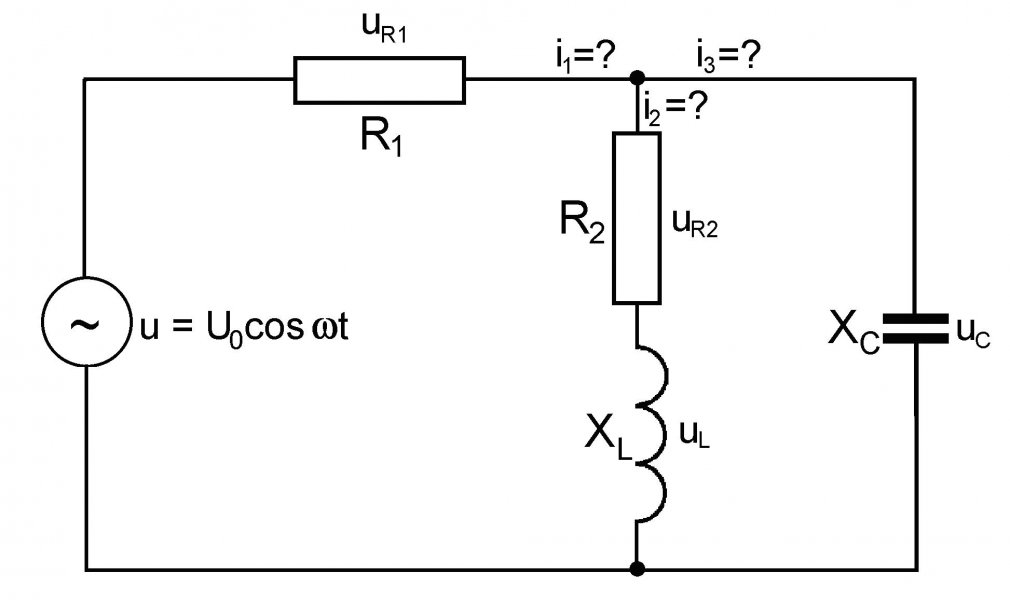
I0 sin(wt + fi). Naopak, ak komplexné číslo i = I0ej(wt + fi) = (I0ejfi)ejwt = I0ejwt = (I0re + j I0im) predstavuje komplexný prúd, potom skutočný prúd je jeho reálnou alebo imaginárnou časťou, ktoré sú navzájom fázovo posunuté o pi/2. Na jednoduchej striedavej elektrickej sieti na obr. 1 ukážeme spôsob aplikácie symbolicko-komplexnej metódy na analýzu siete. Sieť na obr. 1 je prekreslená na obr. 2 do podoby vhodnej pre ďalšie úvahy. V praxi by toto zapojenie mohlo predstavovať napr. nezaťažený jednofázový asynchrónny elektricky motor. Kvôli jednoduchosti numerických výpočtov položíme odpory R1 = R2 = 1 ohm, reaktanciu indukčnosti XL = wL = 1 ohm a takisto reaktanciu kapacity XC = 1/(wC) = 1 ohm. Napäťový zdroj nech má amplitúdu napätia U0 = 10 V a výstupnú impedanciu nulovú, fázový posuv napätia tiež nulový. Frekvencia napätia zdroja pri zadaných hodnotách reaktancií nie je pre ďalší výpočet potrebná, pre úplnosť nech je napr. f = w/(2pi) = 50 Hz (vtedy by bola indukčnosť L = XL/w = = 3,18 mH a kapacita C = 1/(wXC) = 3,18 mF!). Pre zapojenie na obr. 2 platia rovnice
Obr. 2 R1I1 + (R2 + jXL)I2 = U0, (R2 + jXL)I2 + jXCI3 = 0, I1 – I2 – I3 = 0. Pri daných numerických prvkoch zapojenia, prejdú rovnice na tvar I1 + (1 + j)I2 = 10, (1 + j)I2 + jI3 = 0, I1 – I2 – I3 = 0. Je to sústava algebrických rovníc pre komplexné amplitúdy prúdov v troch vetvách danej siete. Riešenia sústavy možno získať bežnými metódami algebry a sú tvaru
I1 = (4 + 2j) A = (20)1/2 e+j arctg(1/2) A = (20)1/2 e+j26,57° A = I1 e+jfi1,
I2 = (2 – 4j) A = (20)1/2 e–j arctg2 A = (20)1/2 e–j63,43° A = I2 e+jfi2, I3 = (2 + 6j) A = (40)1/2 e+j arctg3 A = (40)1/2 e+j71,57° A = I3 e+jfi3. Pomocou týchto výrazov možno vypočítať komplexné amplitúdy napätí na jednotlivých prvkoch v zapojení. Tieto amplitúdy sú UR1 = R1I1 =(4 + 2j) V = (20)1/2 e+j arctg(1/2) V = (20)1/2 e+j26,57° V = UR1 e+jfiR1, UR2 = R2I2 = (2 – 4j) V = (20)1/2 e–j arctg2 V = (20)1/2 e–j63,43° V = UR2 e+jfiR2, UL = jXLI2 = (4 + 2j) V = (20)1/2 e+j arctg(1/2) V = (20)1/2 e+j26,57° V = UL e+jfiL, UC = –jXCI3 = (6 – 2j) V = (40)1/2 e–j arctg(1/3) V = (40)1/2 e–j18,43° V = UC e+jfiC = UR2 + UL. Komplexné amplitúdy prúdov treba vynásobiť s ejwt, čím dostaneme okamžité komplexné prúdy vo vetvách v tvare ii (t) = Ii ejwte+jfii = Ii ej(wt + fii) = Ii [cos (wt + fii)+ j sin (wt + fii)], (i = 1, 2, 3) a ich reálne, alebo imaginárne časti, sú skutočné prúdy. Tie sú iba navzájom fázovo posunuté o 90°. A tak môžeme odpovedať na otázku, aké sú skutočné striedavé prúdy v sieti na obr. 1. Sú to i1 = I1 cos (wt + 26,57°) A = 4,472cos (wt + 26,57°) A, i2 = I2 cos (wt – 63,43°) A = 4,472cos (wt – 63,43°) A, i3 = I3 cos (wt + 71,57°) A = 6,32cos (wt + 71,57°) A. Podobne možno vypočítať okamžité striedavé napätia na jednotlivých prvkoch zapojenia. Tie sú uR1 = UR1 cos (wt + 26,57°) V = 4,472cos (wt + 26,57°) V = R1i1, uR2 = UR2 cos (wt – 63,43°) V = 4,472cos (wt – 63,43°) V = R2i2, uL = UL cos (wt + 26,57°) V = 4,472cos (wt + 26,57°) V = –Ldi2/dt, uC = UC cos (wt – 18,43°) V = 6,32 cos (wt – 18,43°) V = ∫i3dt/C . Treba si všimnúť, že súčet reálnych amplitúd prúdov v uzle sa nerovná nule, tak ako je to v prípade jednosmerných prúdov, nulový je iba súčet komplexných amplitúd (s ohľadom na ich znamienka). V každom okamihu (napr. pri t = 0) pre okamžité hodnoty prúdov ale platí, že i1 – i2 – i3 = 0. Z fázových posunov prúdov sa dá vyčítať, že záťaž zdroja na jeho svorkách má kapacitný charakter (prevažuje účinok kapacity na svorkách zdroja), prúd dodávaný zdrojom predbieha napätie zdroja vo fáze o +26,57°, v indukčnosti prúd zaostáva za napätím zdroja vo fáze o –63,43° a v zvolenej obrovskej kapacite 3,18 mF prúd výrazne predbieha napätie zdroja vo fáze o +71,57°. Napätie uL na indukčnosti predbieha vo fáze napätie uR2 na odpore R2 o 26,57° – (– 63,43°) = 90°, napätie uC na kapacite zaostáva vo fáze za napätím uR2 na odpore R2 a napätím uL na indukčnosti o –18,43° – 26,57° = –45°. Pre prax je najdôležitejšia otázka, aký stredný výkon odovzdáva zdroj jednotlivým odporom, ktorý sa v nich mení na teplo (v indukčnosti a v kapacite, ako je známe, sa nespotrebuje žiadny výkon). Komplexný výkon (pozri v učebnici „Elektromagnetizmus“, kap. 9, ods. 9.5) odovzdávaný do siete je Pkompl = 0,5U0I1* = 0,5×10×(4 – 2j) W = 20 – 10j W. Stredný (reálny) výkon spotrebovaný v sieti je reálnou časťou komplexného výkonu, teda P = Re{Pkompl} = 20 W = 0,5U0I1cos 26,57° W. Imaginárna časť komplexného výkonu je jalový, reaktívny výkon cirkulujúci bez úžitku medzi zdrojom a reaktívnou časťou záťaže (pozri v citovanej učebnici ods. 9.3). V sieti sa prejavuje iba nežiaducim prúdovým zaťažovaním spojovacích vodičov. V energetickej rozvodnej sieti treba robiť opatrenia, aby tento výkon bol minimálny. Na odpore R1 je spotrebovaný stredný výkon P1 = 0,5 I12R1 = 0,5 UR12/R1 = 0,5 I1UR1 = 10 W a na odpore R2 je spotrebovaný stredný výkon P2 = 0,5 I22R2 = 0,5 UR22/R2 = 0,5 I2UR2 = 10 W, teda P = P1 + P2. Treba nakoniec spomenúť, že v elektrotechnike sa niekedy komplexne vyjadrenia napätí, prúdov a impedancií považujú za formálne vektory, nazývané fázory, pomocou nich sa vytvárajú grafické fázorové diagramy, ktoré tiež umožňujú riešiť niektoré elektrotechnické úlohy. Podrobný výpočet úlohy na obr. 1, resp. 2 – takpovediac od podlahy – som urobil preto, lebo mám skúsenosti so študentmi, že väčšinou v dôsledku nepozornosti sa často nevedia dopracovať k správnemu výsledku, ale to je prirodzené – treba sa iba obrniť trpezlivosťou. Dnes riešenia takýchto úloh uľahčujú aj existujúce počítačové programy. V každom prípade – ak sa znovu pozrieme na obr. 1 alebo 2 – tento jednoduchý príklad demonštruje veľké výhody symbolicko-komplexnej metódy. Dúfam, že som Vás úplne neznechutil a želám Vám ešte pekný deň! Autor
27.01.2010 33. Čo je to neper (Np), bel (B), alebo decibel (dB, dBm, dBW)?
Ľudia, ktorí majú vzdelanie v akustike, prípadne v elektrotechnike po prečítaní názvu tejto úvahy sa iba útrpne pousmejú a úvahu čítať nebudú, čo im ani nebudem zazlievať. Avšak pri prednáške o „vysokofrekvenčnej elektronike“, ktorú som konával študentom v 7. semestri, som na začiatku semestra často zistil, že na špecializácii sa našlo dosť študentov, ktorí uvedené pojmy síce počuli, ale ich presné definície nevedeli a nevedeli ich ani používať. Myslím preto, že aj takáto úvaha by niekomu mohla pomôcť. Vo fyzike, ale často aj v matematike treba vyjadriť pomer dvoch rozmerovo rovnakých veličín, ktoré sú často závislé od ďalších parametrov (v elektrotechnike najčastejšie od frekvencie). Niekedy je to pomer veličín, ktoré sa líšia o mnoho radov. Takýto pomer A je bezrozmerné číslo a je napr. tvaru A= I/I0, (1) kde I a Io môžu byť v akustike napr. intenzita zvuku vo W/m2, či akustický tlak v pascaloch (Pa), v elektrotechnike napr. amplitúdy napätí, prúdov, výkonov, prípadne impedancii. Veličina Io je niekedy vzťažná (referenčná), I je priebežná. ***** V akustike veličina, ktorá charakterizuje prenos zvuku je napr. intenzita zvuku. Je to množstvo zvukovej energie, ktorá prejde danou plochou za jednotku času (W/m2) a predstavuje akustický výkon, ktorý pôsobí na ušný bubienok. Testy ukazujú, že človek vníma zvuk až od istého, prahového akustického tlaku, pričom hodnota intenzity závisí od mnohých faktorov ako napr. od teploty (so vzrastajúcou teplotou mierne rastie rýchlosť zvuku) a od vlhkosti vzduchu, ale predovšetkým od frekvencie zvuku a od veku a kondície počúvajúceho. Je to teda veličina silne subjektívna. Pre frekvenciu 1 kHz prahová intenzita (prah počuteľnosti) je cca I0 = 10-12 W/m2. Táto hodnota bola zvolená ako štandard; skutočný, tzv. absolútny prah počuteľnosti sa od nej môže líšiť z dôvodov uvedených vyššie. Treba ešte pripomenúť, že zdravé ľudské ucho vníma zvuky vo frekvenčnom intervale asi od 15 Hz do asi 20 kHz. Intenzity zvukov s ktorými ľudia prichádzajú do styku v bežnom živote sú ale neporovnateľne vyššie. Už len bežný hovor v reštaurácii je spojený s intenzitami zvukov cca 10-6 W/m2, teda asi miliónkrát vyššia ako prahová intenzita. Bežný pouličný hluk električiek a aut odpovedá intenzite zvuku cca 10-4 W/m2, je teda asi 108-krát vyššia ako prahová intenzita a štartujúce prúdové lietadlo produkuje hluk s intenzitou vyššou ako 1 W/m2, teda asi 1012-krát vyššou ako prahová. Je to prah bolesti. Z povedaného vidieť, že hladiny hlukov A dané výrazom (1) môžu prekrývať mnoho radov a teda daný výraz nie je vhodný na číselné vyjadrenie hluku. ***** Podobná situácia býva v elektrotechnike. V elektrotechnike sú známe rôzne zapojenia, ktorých blokové zobrazenia vedú na známe dvojbrány (to čo sa voľakedy volalo "štvorpól", dnes sa volá "dvojbrán", pozor – nie dvojbrána!). Spoločným znakom dvojbránov sú štyri prívody do bloku, spojené do dvojíc. Obyčajne sú to dvojice vstupných a výstupných svoriek. Ako príklad možno uviesť rôzne typy frekvenčných filtrov, alebo zosilňovačov, prípadne zoslabovačov (atenuátorov). Na dvojbránoch možno definovať frekvenčne závislý koeficient prenosu podobným výrazom, ako je výraz (1), teda napríklad A(f)= Pvýst(f)/Pvst(f). kde Pvst(f) a Pvýst(f) sú vstupné a výstupné výkony závislé od frekvencie f. Závislosť vyjadrená posledným výrazom je frekvenčná charakteristika dvojbránu, pričom frekvencia sa obyčajne mení cez mnoho rádov. Pri takýchto rádových zmenách frekvencií sa aj koeficient prenosu obyčajne mení rádovo, a to vedie k rovnakým problémom ako vyššie uvedený príklad z akustiky. Už škótsky matematik, astronóm&astrológ John Napier (1550 – 1617), pôvodca prirodzených logaritmov prišiel na myšlienku, vyjadrovať takéto veličiny ich logaritmami. A tak namiesto pomeru dvoch veličín, ktoré sú v nejakom príčinnom vzťahu (ako napríklad vstupné a výstupné napätie, prúd alebo výkon v nejakom dvojbráne) berie sa podľa dohody logaritmus uvažovaného pomeru. Tak napríklad v prípade dvoch výkonov Pvýst a Pvst možno namiesto ich pomeru A = Pvýst/Pvst, ktorý predstavuje zosilnenie alebo útlm výkonu, pracovať s veličinou A = ln(Pvýst/Pvst) (Np), (2) ktorá v prípade zosilnenia, keď Pvýst > Pvst je kladná a v prípade útlmu, keď Pvýst < Pvst je záporná. Veličina A je bezrozmerná, napriek tomu má jednotku nazvanú neper (Np) na počesť Johna Napiera. Je zrejmé, že ±1 Np je zosilnenie alebo útlm výkonov v pomere Pvýst/Pvst = e = 2,718 281 8 ..., kde e je základ prirodzených logaritmov. Ak sa pozrieme na výraz (2) vidíme, že prirodzený logaritmus vo výraze nie je vhodný, pretože výsledky sú necelé čísla a tak americký fyzik a fyziológ škótskeho pôvodu Alexander Graham Bell (1847 – 1922) navrhol namiesto prirodzeného logaritmu použiť vo vzorci (2) dekadický logaritmus, a výraz (2) prešiel na tvar A = log(Pvýst/Pvst), (B) (3) Jednotkou takto zavedeného pomeru je bel (B) na počesť Alexandra Grahama Bella. Jednotka bola pôvodne zavedená na vyjadrenie akustického tlaku, resp. výkonu. Hodnota ±1 B predstavuje desaťnásobné zosilnenie alebo desaťnásobný útlm výkonu. V prípade, ak je porovnávanou veličinou napätie alebo prúd, treba pravú stranu výrazu (3) vynásobiť s faktorom 2, pretože výkon je úmerný druhej mocnine napätia alebo prúdu. Je to však možné iba vtedy, ak vstupná a výstupná impedancia dvojbránu sú rovnaké. Jednotka bel je príliš veľká, a preto sa v praxi častejšie pracuje s jej desatinou, ktorá sa nazýva decibel (dB), teda 1 B = 10 dB. Pravú stranu výrazu (3) treba vynásobiť súčiniteľom 10 a v prípade napäťových alebo prúdových veličín súčiniteľom 20. Podľa uvedeného možno teda napr. koeficient prenosu vyjadriť A = 10log(Pvýst/Pvst) = 20log(Uvýst/Uvst) = 20log(Ivýst/Ivst), (dB) (4) Vlastnosti frevenčných charakteristík filtrov (ich asymptoty) sa udávajú v dB/na dekádu (frekvencií), alebo v dB/na oktavu. V elektrotechnike je oktávou frekvenčný interval v pomere frekvencií 1:2. Pojem je prebraný z hudobníckej terminológie. Logaritmické vyjadrenie výkonov v elektrotechnike má ešte jednu výhodu Ak je zaradených za sebou niekoľko zariadení (dvojbránov) výsledný priamy koeficient prenosu je produktom (násobkom) koeficientov jednotlivých dvojbránov. Pri logaritmickom vyjadrení sa jednotlivé koeficienty sčítajú. Pre pasívne RL-, alebo RC-filtre (pozri napr. „Elektromagnetizmus“, kap. 7, odsek 7.8 a kap. 9, odsek 9. 8.1 tu), pre ktoré je koeficient prenosu A < 1, pôsobí ako tlmenie (útlm), v decibeloch je záporný, teda A < 0. Zosilňovače, majú zosilnenie (zisk) väčší ako 1, teda A > 1, v decibelovej stupnici zisk je kladný, teda A > 0. V tabuľke je uvedených niekoľko typických hodnôt koeficientu prenosu (útlmy, prípadne zisky) a ich odpovedajúce hodnoty v dB. Dobre si je všimnúť, že vzostup, alebo pokles výkonového signálu faktorom 2 (napäťového, alebo prúdového signálu faktorom 21/2) odpovedá v decibelovej stupnici ±3 dB (pozri výraz (4)). Samozrejme ±3 dB je približná hodnota, pretože log2 nie je 0,3, ale 0,30102999..., čo ale pre prax je nepodstatné. Tabuľka A 10-3 1/2 1/21/2 1 21/2 2 10 103 A[dB] -60 -6 -3 0 3 6 20 60 Pozrime sa teraz aké akustické výkony produkujú vyššie uvedené akustické zdroje v dB. Tieto výkony možno vypočítať z výrazu A = 10log(I/Io) (dB) (5) Možno sa presvedčiť, že pri Io = 10-12 W/m2, ak intenzita zvuku je prahová, teda I = Io, potom výkon A = 0 dB. Hovor v reštaurácii (I = 10-6 W/m2) odpovedá výkonu A = 60 dB, silný pouličný hluk (I = 10-4 W/m2) odpovedá hodnote výkonu A = 80 dB a hluk štartujúceho prúdového lietadla (I = 1 W/m2) odpovedá hodnote A = 120 dB, čo je už spomínaný prah bolesti. ***** V telekomunikácii, kde sa pracuje s výkonmi rádovo 1 mW až 1 W sa ako referenčný výkon vo výraze (4) berie výkon Pvst = 1 mW, alebo Pvst = 1 W. Ak referenčný výkon Pvst = 1 mW, výstupný výkon udáva úroveň v jednotkách dBm výrazom P(dBm) = 10 log Pvýst(mW), (6) takže napr. výstupnému výkonu 1 mW odpovedá úroveň 0 dBm, 2 mW odpovedá 3 dBm, 10 mW odpovedá 10 dBm atď. Podobne ak Pvst = 1 W, potom výstupnému výkonu 1 W odpovedá úroveň 0 dBW, 2 W odpovedá 3 dBW, 10 W odpovedá 10 dBW atď. Aj keď v SI-sústave je neper zakázanou jednotkou je dobre uviesť, že medzi výkonom zadaným v neperoch, teda A(Np) a výkonom v decibeloch A(dB) platí vzťah A(dB) = 20 (log e) A(Np) = 8,686 A(Np), takže 1 Np = 8,686 dB = 0,8686 B a 1 dB = 0,1151 Np = 0,1 B. Aj jednotky dBm a dBW sú v SI-sústave zakázané. ***** Nakoniec bude užitočné uviesť niekoľko výkonov v dBm z rôznych pozemských aj vesmírnych zdrojov vypočítaných podľa vzťahu (6): 1) 80 dBm (100 kW = 108 mW) - typický prenášaný výkon z FM vysielača vo vzdialenosti 50 km. 2) 60 dBm (1 kW = 106 mW) - typický výkon mikrovlnovej rúry, - maximálny RF výkon amatérskych vysielačov bez speciálneho povolenia. 3) 50 dBm (100 W = 105 mW) - typické tepelné žiarenie emitované ľudským telom. 4) 15 dBm (32 mW) - typický WiFi výkon prenášaný do rooterov notebookov. 5) −60 dBm (1 nW/m2 = 10-6 mW/m2) - tepelné žiarenie dopadajúce na meter štvorcový povrchu Zeme z ves- mírneho objektu magnitúdy +3,5 (Hmlovina Andromédy). 6) −111 dBm (0.008 pW = 8 fW = 8.10-12 mW) - tepelné šumové pozadie GPS kanálu v pásme šírky 2 MHz.. 7) −127.5 dBm (0.178 fW = 178 aW = 178.10-15 mW) - typický prijímaný signál z GPS satelitov. 8) −174 dBm (0,004 aW = 4 zW = 4.10-18 mW) - typické tepelné šumové pozadie v pásme 1 Hz pri izbovej teplote 20o C. 9) −192.5 dBm (0.056 zW = 56 yW = 56.10-21 mW) - tepelné výkonové šumové pozadie vonkajšieho vesmíru v pásme šírky 1 Hz. Je to zvyškové - reliktné žiarenie, ktoré "blúdi" vesmírom od big bangu (veľkého tresku), teda asi 15 miliárd rokov. Reliktové žiarenie objavili v roku 1965 Arno Penzias a Robert Wilson a v roku 1978 za tento objav získali Nobelovu cenu za fyziku. Reliktové žiarenie svojimi charakteristikami odpovedá žiareniu absolútne čierneho telesa okolo teploty 2,73 K. Žiarenie je všesmerové a najväčšiu intenzitu má pri vlnovej dĺžke 2-3 milimetrov. Objav reliktového žiarenia bol silným argumentom podporujúcim teóriu veľkého tresku. 10) −∞ dBm (0 W = 0 mW) - nulový výkon . Význam symbolov súčiniteľov vo vyjadrení rádov výkonov: p - pico - 10-12, f - femto - 10-15, a - atto -10-18, z - zepto - 10-21, y - yocto 10-24. (Symboly prebrané z internetovej encyklopédie Wikipédia). Želám Vám všetkým dobrý deň a príjemnú jeseň! Autor 24.10.2010
34. James Clerk Maxwell
Pri štúdiu tejto prekrásnej teórie,
človek má pocit, že rovnice v nej žijú
samostatným životom, že majú vlast-
nú inteligenciu, ako by boli múdrejšie
ako my sami, dokonca ako ich pô-
vodca. Akoby nám dávali viac, než bo-
lo svojho času do nich vložené.
Heinrich Hertz
V našich predchádzajúcich úvahách meno James Clerk Maxwell bolo uvádzané veľmi často a možno povedať, že vo fyzikálnych vedách sa nemnohým podarilo vykonať toľko, ako práve Maxwellovi v jeho relatívne krátkom živote. Písať o Maxwellovi je ťažká úloha, pretože o ňom bolo popísané veľmi veľa a je k tomu ťažké niečo pridať, čo by nepôsobilo ako klišé. Napriek tomu to chcem urobiť, pretože jednoducho si myslím, že do tohto môjho súboru úvaha o Maxwellovi patrí – už aj z úcty k jeho dielu. Chcem sa však pokúsiť ukázať aj iné, osobnostné a charakterové vlastnosti tohto vynikajúceho človeka.
James Clerk Maxwell (1831 – 1879) Mladý Maxwell na Trinity College v Cambridge.
V rukách drží jeden z jeho farebných kotúčov.
James Clerk Maxwell, škótsky fyzik sa narodil 13. júna 1831, v roku keď Faraday objavil elektromagnetickú indukciu a zomrel 5. novembra 1879, v roku, keď sa narodil Albert Einstein. Maxwell bol dokonalým prepojením medzi tými dvoma veľkými fyzikmi a ich érami. Narodil sa v Edinburgu v dobre známej škótskej rodine. Meno Clerk je po otcovi, ktorý bol právnik, meno Maxwell po matke, ktorá mu však umrela, keď mal 9 rokov. Vychovával ho otec a teta. Už v mladosti sa prejavil ako veľký matematický génius, čo mu medzi spolužiakmi vynieslo prezývku „strelený“. Maxwell mal nielen výnimočné schopnosti vykonávať matematické abstrakcie, ale aj mimoriadnu zvedavosť, ako veci fungujú, na základe čoho, vyrábal funkčné modely rôznych prístrojov a zariadení. Bol teda netypický teoretik! Stále bombardoval starších otázkami typu: „Ako to funguje?“, alebo „O čo tu vlastne ide?“
Edinburghská akadémia, Edinburghská Univerzita
ktorú Maxwell navštevoval ako žiak
V roku 1847 sa Maxwell zapísal na Univerzitu v Edinburgu, a v roku 1850 prešiel na Trinity College Univerzity v Cambridge, kde bol v roku 1854 graduovaný v matematike ako druhý v triede. V roku 1856 prijal ponuku miesta profesora na Marischal College v Abardeene v Škótsku, hlavne aby bol v blízkosti otca, ktorého si veľmi vážil,. Otec však bol chorý a zomrel krátko predtým ako syn na toto miesto nastúpil. O dva roky neskôr sa Maxwell oženil s Katherinou Mary Dewar, ktorej otec bol principálom na Marischal College. Po piatich rokoch (1860 – 1865) na Kings´s College v Londyne odišiel Maxwell do čiastočného dôchodku a usadil sa na rodinnom sídle Glenlair blízko dedinky Parton v Škótsku. Tu sa venoval výskumu hlavne v elektromagnetizme. V roku 1871 Maxwell prijal ponuku aby vytvoril a viedol Cavendishovo Laboratórium, prvé experimentálne laboratórium na Univerzite v Cambridge. Tu Maxwell začal tradíciu, ktorá poznačila experimentálnu fyziku v Cambridge. Maxwell sa podpísal pod práce v rôznych oblastiach fyziky. Okrem iného vypracoval závažnú štúdiu o kinetickej a štatistickej teórii plynov (štatistické Gaussovo rozdelenie molekúl plynu podľa rýchlosti, stredná voľná dráha molekúl), spracoval teóriu farebného videnia, dôležité sú jeho práce v termodynamike, v astrofyzike vyriešil záhady prstencov okolo Saturna, urobil závažné práce v hydrodynamike a v teórii pružnosti. Zaviedol pojmy ako mechanické napätie, deformácia, mechanický tlak, víry v kvapalinách a plynoch, a mnohé iné. Počas celého života Maxwell krok za krokom rozvíjal a dovádzal do dokonalosti svoju veľkú ideu o elektromagnetickom poli. Prvé výsledky tohto výskumu tvoria práce v Maxwellovom diele „O Faradayových siločiarach“ (On Faraday’s Lines of Force) napísaneho v roku 1855, ale publikovaného až v roku 1864. Využijúc mechanické analógie vyjadril známe vzťahy elektrodynamiky matematickým jazykom odpovedajúcim modelom Faradaya. Matematický aparát prebral od írskeho matematika W. R. Hamiltona (1805 – 1865) (Hamilonov operátor!).
Prvá farebná fotografia vyhotovená Maxwellova pohľadnica.
J. C. Maxwellom v roku 1861. priateľovi Petrovi Taito vi
Už v prvej etape svojich výskumov v elektromagnetizme bol presvedčený, že teória pôsobenia na diaľku nemôže neprotirečivo objasňovať elektromagnetické javy. Ucelená teória elektromagnetizmu je obsiahnutá v najznámejšom jeho diele „Treatise on Elektricity and Magnetism“ (Pojednanie o elektrine a magnetizme), ktorá v prvom vydaní vyšla v roku 1873 a odvtedy nespočetne krát a v mnohých jazykoch. Jadrom diela je dvadsať rovníc medzi štyrmi vektormi poľa E, B, D, H, nábojovou hustotou ro a prúdovou hustotou J, ktoré Oliver Heaviside (1850 - 1925) spolu s Heinrichom Hertzom (1857 – 1893) neskôr prepísali do štyroch vektorových rovníc dnes známych ako Maxwellove rovnice (pozri napr."Elektromagnetizmus", kap. 8, ods. 8.7, tu). Posledná etapa elektrodynamických výskumoch Maxwella je charakterizovaná jeho veľkou o syntézu elektromagnetizmu a optiky. Maxwellova elektromagnetická teória hneď od jej vzniku umožňuje riešiť nielen elektrické, ale aj mnohé praktické úlohy optiky: určenie indexu lomu materiálov n = (mir.epsilonr)1/2 a napr. určenie indukčnosti a vzájomnej indukčnosti cievok v elektrotechnike. V práci o dielektrikách Maxwell prišiel s pozoruhodnou hypotézou o posuvnom prúde známom aj ako Maxwellov prúd (pozri napr. "Elektro-magnetizmus", kap. 6, ods. 6.3, tu). Hypotézu o posuvnom prúde experimentálne dokázal v roku 1887 nemecký fyzik Heinrich Hertz na Univerzite Karlsruhe, dôkazom existencie elektromagnetických vĺn. Bez existencie toho, čo nazývame posuvným prúdom, by elektromagnetické vlny neexistovali. Vytvorením teórie elektromagnetizmu sa Maxwell domnieval, že elektromagnetické pole musí existovať v substancii, ktorú nazval éter – všetko prenikajúce prostredie s absolútne nehybným systémom v ktorom sa odohrávajú všetky fyzikálne deje. Stimuloval vedcov experimentálne dokázať existenciu tohto nehybného éteru. V roku 1881 takýto pokus vykonal A. Michelson (1852 – 1931) a ako je známe výsledok pokusu bol negatívny. Dilému vyriešil mladý Albert Einstein (1879 – 1955) svojou špeciálnou a neskôr všeobecnou teóriou relativity. Popri iných revolučných fyzikálnych teóriách vzniknutých v 19. a 20. storočí ako už spomínaná špeciálna a všeobecná teória relativity, kvantová mechaniku a i., elektromagnetizmus s Maxwellovymi rovnicami zostanú navždy najdôležitejšou súčasťou fyziky pre jeho neobyčajne širokú škálu praktických aplikácií. Meno James Clerk Maxwell nikdy neupadne do zabudnutia.
James a Katherine Maxwell, 1869 James Clerk Maxwell - pozoruhodný vedec bol jemný, religiózny, nesebecký a obetavý muž, mal rad deti (s manželkou vlastné nemali), svojich príbuzných a priateľov. Raz napísal: „Čítanie je dobré, práca je vynikajúca, ale lepšie je mať dobrých priateľov“. O manželku, ktorá bola chorľavá sa príkladne staral, pričom sám bol vážne chorý, čo utajoval prakticky až dokonca života. Mal zmysel pre jemný anglický humor. Na prednáške o novo objavenom telefóne urobil o ňom vtipnú poznámku: „je to perfektne symetrická aparatúra – v strede je drôt, na jeho koncoch sú telefónne prístroje a pri nich dve klebetnice“.
Maxwellova životná cesta skončila, keď 5. novembra 1879, vo veku 48 rokov podľahol rakovine. Po rozlúčke v Trinity College v Cambridge previezli rakvu s pozostatkami Jamesa Clerka Maxwella do dedinky Parton neďaleko rodinného sídla Glenlair. Pochovali ho vedľa rodičov vo dvore malého kostolíka, postaveného aj z Maxwellovych darov. „Maxwellove práce obstáli v najnáročnejšej skúške – skúške času. Každý rok, ktorý uplynie od jeho smrti, nás núti, aby sme si stále viac a viac uvedomovali jeho prínos do fyziky. Výsledky práce Maxwella, ktoré dal do služieb ľudstva, vidíme z roka na rok ako stále závažnejšie.“ S pozdravom pre mojich čitateľov! Autor 27.10.2010 (Životopisné údaje prevzaté z Wikipédie).
35. Vychádza monografia „Elektromagnetizmus“ !!! Milí priatelia!
To, čo Vám chcem napísať vlastne ani nie je úvaha, ale skôr informácia, že konečne po viac ako desiatich rokoch od prvého vydania sa našiel vydavateľ, ktorý sa bez sponzora rozhodol monografiu "Elektromagnetizmus" vydať (mnohí autori ešte aj dnes "elektromagnetizmus" nazývajú – "elektrina a magnetizmus"). Vydavateľ nedostal na vydanie žiadne finančné prostriedky od nikoho, tým menej od Ministerstva školstva, vedy, výskumu a športu SR. Škoda – knižka by pre študentov mohla vyjsť lacnejšie! Za ochotu ísť do rizika som vydavateľovi nesmierne povďačný. Verím, že riziko nie je veľké, pretože už teraz som dopytovaný, kedy kniha vyjde. Čo sa týka knižky samotnej, samozrejme už to nie je tá, z pred desiatich rokov. Nenechal som ju celý ten čas "ležať ladom". Predovšetkým som v nej odstraňoval chyby a menil niektoré formulácie, vymenil som veľké množstvo obrázkov a takmer všetky fotografie (to je veľká výhoda elektronickej verzie). V knihe som nenašiel veľa chýb, ale pri asi 16 000 matematických výrazoch, sa ich tam niekoľko predsa len našlo. Nechcem tvrdiť, že knižka už nemá žiadne nedostatky, verím však, že počet chýb – ako som napísal v predslove k učebnici – bude postupne konvergovať k nule. Pri dnešnej tlačiarenskej technike praktický každý výtlačok knihy môže byť originálom. Kniha sa momentálne tlačí a mala by byť k dispozícii do konca mesiaca. Jej cena ešte nie je stanovená. Žiaľ musím Vám oznámiť, že z komerčných dôvodov nemôže elektronická verzia knižky zostať na internete. To viete – vydavateľ, ale aj autor majú záujem, aby sa kniha predávala, na čo majú právo. Nech Vás ale teší skutočnosť, že konečne dostanete do rúk knihu z fyziky na kvalitnom papieri, v krásnej výtvarnej úprave a v tvrdej väzbe. Vydavateľ to robí profesionálne a s vysokým stupňom elegancie. V mojich študentských časoch bolo samozrejme, že sme si ako študenti budovali osobné knižnice. Dnešní absolventi po skončení štúdia odchádzajú z fakúlt bez jedinej knihy. Je pravda, že z fyziky sa dnes takmer nič nevydáva. Vtedy na knižnom trhu bolo relatívne veľa odborných kníh a boli neporovnateľne lacnejšie. Okrem toho bol tu objemný trh s ruskými knihami, na ktorom boli preklady všetkého, čo odborné vyšlo na západe, a stalo za preklad (aspoň niečo bolo dobré aj v minulom režime, ale nebolo toho veľa). Počul som už názor, že medzi študentmi-elektroinžiniermi sa kniha nebude veľmi predávať, pretože majú iba 2 semestre fyziky (!) – predmetu, ktorý je pre nich profilujúci. Ale práve preto by si budúci inžinieri knihu mali kúpiť, aby sa to, čo ich nenaučili na fakulte, mohli doučiť doma, alebo pred štátnicami, prípadne aj neskôr. To platí aj pre iné, nefyzikálne odbory. Okrem toho pre elektroinžinierov kniha môže slúžiť ako úvod do teórie elektrických sieti a teórie prenosových vedení. Knihu o elektromagnetizme som sa snažil písať tak, aby na čitateľa nepôsobila suchárskym dojmom. Práve toto sa fyzike často vytýka. Na vine ale nie je fyzika, ale často učitelia fyziky. Učiteľ musí byť schopný odpovedaľ na každú otázku študenta, ak nie okamžite, tak pri najbližšej príležitosti. Ak sa študentovi odpovede nedostane, stratí o výklad zaujem a to môže byť začiatok averzie a nezáujmu o fyziku. Chcel som, aby kniha čitateľa skôr príťahovala, ako nezrozumiteľnosťou a "učenosťou" odpudzovala. Okrem toho, je vždy lepšie napísať menej a jasne, ako veľa a ešte k tomu veľmi učene. Preto som pojal do knihy to z elektromagnetizmu, čo sa tam únosne zmestilo a čo považujem z môjho pohľadu za nevýhnutné. Myslím, že kniha je napísaná tak, že sa dá čítať aj bez počúvania prednášky – to však vôbec neznamená, že prednášky treba ignorovať. Ponuku knihy najdete na stranke http://www.iris-knihy.biznisweb.sk/product/elektromagnetizmus-1426/ Pre tých, ktorí knihu nepoznajú uvádzam anglickú anotáciu v tiráži knihy a niekoľko myšlienok z posudkov recenzentov: ***** “This textbook is a comprehensive introduction to the study of electromagnetic phenomena at the undergraduate level. The book is suitable to students of physics and electrical engineering at the universities, technological institutes, partly to students of chemistry, biology, medicine, agriculture, etc. The textbook can also be useful for postgraduate students, scientists and for all interested in modern approaches to the electromagnetic theory. Besides the classical parts of electromagnetism like the electrostatics, magnetostatics and electrodynamics the book deals with such modern subjects of electromagnetism like the superconductivity, Josephson effect, quantum Hall-effect, electron-spin resonance (ESR), nuclear magnetic resonance (NMR) as a modern tool of medical diagnostics. Various elder and recent methods of the measurements of the velocity of the light are described. Special attention is paid to the magnetism of matter, modern magnetic materials and their investigation and applications. In the chapters dealing with alternating current and electromagnetic waves the electric networks and transfer of electromagnetic signals by transmission lines is described in some detail. The textbook involves the fundamentals of vector algebra and some differential operations on scalar and vector fields. Detailed explanation of concept of gradient, divergence and curl are also given. The essential mathematical prerequisites for the subjects discussed in this book are integral calculus, linear real and complex algebra. Some acquaintance with differential equations would be helpful, but not strictly essential. The textbook includes 326 selected and solved problems”. ***** Z posudkov recenzentov: Tirpákova kniha ... nie je obyčajnou učebnicou, ale má v sebe prvky monografie adresovanej tak začínajúcim adeptom fyziky, prípadne elektrotechniky, ako aj starším už skúseným výskumníkom, učiteľom a ďalším čitateľom. Štýl je pútavý, kniha je dobre ilustrovaná aj portrétmi mnohých slávnych fyzikov. ... "Fajnšmekri" si zgustnú na odkazoch na literatúru, uvedených v texte. ... V prospech Tirpákovej knihy hovorí jej vysoká odborná kvalita a množstvo riešených príkladov. ... Aj dobrí znalci problematiky nájdu v knihe informácie, ktoré môžu považovať za poučné a ktoré sa napríklad v časoch ich vysokoškolského štúdia v učebnici nemohli vyskytovať ... Text Tirpákovej knihy je osviežený osobnými postrehmi autora, čo jej dáva punc originálnosti ... Tí zo študentov, ktorí majú záujem o hlboké vedomosti si zákonite uvedomia vysokú informačnú hodnotu a kvalitu Tirpákovej monografie a ľudia z univerzitných pracovísk, z ústavov SAV a rezortných výskumných inštitúcii môžu mať z čítania Tirpákovej knihy veľké intelektuálne potešenie. ... Keďže je sotva reálne predpokladať, že v rámci základného štúdia sa študenti stihnú naučiť všetko, čo Tirpákova kniha obsahuje, predvídam, že táto kniha bude slúžiť ako dobrý učebný text aj pre doktorandské štúdium. Prof. RNDr. Viktor Bezák, DrSc.
Okrem matematicko-fyzikálnych fakúlt učebnica poslúži aj pri výučbe fyziky na technických univerzitách a tiež ju privítajú všetci zaujemcovia o elektromagnetické javy, a to nielen fyzici, ale aj inžinierski a technickí pracovníci v priemysle. ... Veľmi dôkladnou a zaujímavou je kapitola ... o magnetických vlastnostiach látok, obsahujúca pôvodné názory autora. ... magnetizačný vektor J (vektor magnetickej polarizácie) považuje autor za nadbytočný a v texte ho nepoužíva. ... Autor je fyzikálnej verejnosti dobre známy odborník najmä na magnetizmus látok o čom publikoval doma a v zahraničí rad pôvodných vedeckých pojednaní ... Ako učiteľ pracoval dlhší čas aj v zahraničí. ... Za veľkú prednosť ... považujem skutočnosť, že ... autor používa symbolicko-komplexnú metódu bežnú pri analýze striedavých prúdov elektrotechnikmi. ... Treba oceniť kapitoly o moderných fyzikálnych javoch ako sú supravodivosť (aj vysokoteplotná), Josephsonov jav, jadrová a elektrónová paramagnetická rezonancia (NMR a EPR) a i. ... Riešené úlohy sú veľmi významným počinom autora, pretože pripravujú čitateľa na riešenie skutočných problémov fyzikálnej a inžinierskej praxe. ...Ide skutočne o pozoruhodné dielo! Prof. Ing. Matej Rákoš, DrSc. ***** Milí mladí priatelia! Verím že sa Vám knižka bude páčiť a že po skončení štúdia Vám bude pripomínať krásne študentské časy. Autor 22.1. 2011
|