Elektromagnetické javy a ich miesto v elektronike

úvaha 16-20 |
|
OBSAH:
16. Ako sa vyberá vlnová impedancia koaxiálneho vedenia určeného na prenos internetu a káblovej televízie? 17. Aký je rozdiel medzi sériovou a paralelnou rezonanciou?
18. Čím sa líši prenos elektromagnetickej energie mikrovlnovými obvodmi od prenosu
nízkofrekvenčnými obvodmi?
19. Niekoľko úloh s kondenzátormi.
20. Ako vysoko nad povrchom Zeme musia "visieť" geostacionárne družice?
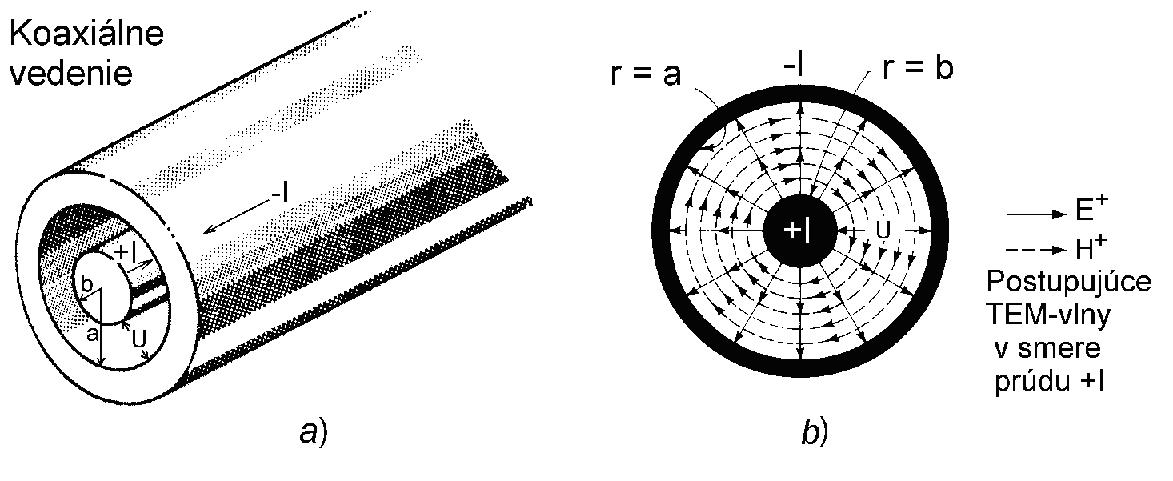
16. Ako sa vyberá vlnová impedancia koaxiálneho vedenia
určeného na prenos internetu a káblovej televízie?
Pri zavadzaní káblových sieti na prenos televíznych programov a internetu do bytov si možno aj menej zorientovaný užívateľ všimol, že inštalované koaxiálne vedenie (nesprávne "koaxiálny kábel") má na povrchu izolácii nejaký údaj – napríklad 75 ohmov, alebo 50 ohmov. Tento údaj sa nazýva „vlnová impedancia vedenia“ (nesprávne „vlnový odpor kábla“). Otázkou je, čo takýto údaj vlastne znamená. Pri odpovedi na túto otázku treba trochu širšie analyzovať otázku prenosu elektromagnetického výkonu medzi jeho zdrojom (napr. galvanický článok, alebo elektráreň) a záťažou zdroja (spotrebič elektrickej energie). Zo stredoškolskej fyziky je známe, že elektrický výkon, ktorý dodáva jednosmerný, alebo nízkofrekvenčný zdroj s vnútornou impedanciou Zi do záťaže s impedanciou Z je maximálny vtedy, keď Z = Zi, t.j. keď impedancia záťaže sa rovná vnútornej impedancii zdroja. Predpokladáme, že vedenie spájajúce zdroj a záťaž je bezstratové a že jeho dĺžka je podstatne menšia ako vlnová dĺžka odpovedajúca frekvencii napätia zdroja. Dodávaný výkon do záťaže je vtedy maximálny, ale je iba polovicou celkového výkonu zdroja, druhá polovica sa spotrebuje na vnútornej impedancii zdroja. Pri všetkých iných hodnotách Z je výkon odovzdávaný záťaži ešte menší a blíži sa k nule, ak Z → 0, alebo ak Z → nekonečna (pozri „Elektromagnetizmus“, kap. 5). Stav maximálneho odovzdávania výkonu do záťaže sa nazýva „stav prispôsobenia impedancie záťaže impedancii zdroja“ (angl. – matching of impedances). Aj keď sa na prvý pohľad zdá, že to je režim, v ktorom zdroje elektrickej energie pracujú, je to režim vrcholne neekonomický, keď účinnosť prenosu energie do záťaže je iba 50 %. Tento režim sa využíva iba výnimočne, keď do záťaže, počas krátkej doby, treba dodať maximálny možný výkon. Je to napríklad prípad spúšťania motora automobilu pomocou akumulátora a spúšťača (obidve zariadenia majú veľmi nízky vnútorný odpor). Energetická sieť musí pracovať čo možno s najvyššou účinnosťou, keď – obrazne povedané – vnútorná impedancia elektrárne je oveľa menšia ako výsledná impedancie všetkých záťaži elektrárne.
Obr. 1 Iná je situácia pri prenose elektromagnetickej energie na vysokých, alebo veľmi vysokých frekvenciách (decimetrové a centimetrové vlny). Zatiaľ čo výkon a energia na nízkych frekvenciach sa prenášajú napätím a prúdom, na veľmi vysokých frekvenciách sa energia prenáša vysokofrekvenčným elektromagnetickým i vlnami. Pri prenášaní vysokofrekvečnej energie nejde ani tak o maximálny prenesený výkon, ale skôr o zamedzenie odrazov vĺn na záťaži a tým vzniku stojatých vĺn na vedení. Vysokofrekvenčný výkon sa prenášaný dutinou vlnovodu, alebo dielektrikom koaxiálneho vedenia (pozri obr. 1). Prenosové vedenia sú teda ďalšie prvky, ktoré sa zúčastňujú pri prenose vysokofrekvenčnej energie oproti prenosu jednosmernej, prípadne nízkofrekvenčnej energie, kde vystupuje iba zdroj a záťaž. Vo vlnovodoch a v koaxiálnych vedeniach môžu vzniknúť odrazy energie, nasledne vznikne stojatá vlna, ktorá nepriaznivo ovplyvňujú prispôsobenie, aj za predpokladu, že impedancie zdroja a záťaže sú rovnaké. Vedenie musí teda spĺňať isté predpoklady – ináč povedané – musí mať istú vlnovú impedanciu, ktorú možno definovať nasledovným spôsobom: Pod pojmom „vlnovou impedanciou vedenia Zv“ budeme rozumieť pomer amplitúd napätia U+ a prúdu I+, alebo amplitúd elektrického E+ a magnetického poľa H+, na nekonečne dlhom koaxiálnom vedení. Na takom vedení je iba od zdroja postupujúca elektromagnetická vlna (neexistuje žiadny odraz). Okrem toho sa predpokladá, že na vedení sa šíri iba transverzálne elektromagnetická (TEM) vlna od nulovej po hraničnú frekvenciou fmax a žiadne vyššie módy. Rovnaké vlastnosti, ako nekonečné vedenie, má aj vedenie konečnej dĺžky, ak sa na jeho koniec pripojí záťaž, ktorej impedancia je taká, že na vedení nespôsobuje odrazy. Záťaž s takou impedanciou sa nazýva prispôsobená záťaž (matched load). Pojem „vlnová impedancia vedenia“ možno definovať aj ako impedanciu, ktorá sa rovná impedancii prispôsobenej záťaže, pri ktorej na vedení nevzniká odrazená vlna. Systém: zdroj – vedenie – záťaž bude teda prispôsobený, ak všetky tri impedancie sú rovnaké. Mierou prispôsobenia vedenia je aj stojatá vlna, ktorá vzniká ako superpozícia odrazenej a postupujúcej vlny. Na vedení, ktoré je zakončené prispôsobenou záťažou stojatá vlna nevznikne (pozri „Elektronika veľmi vysokých frekvencii“ na tejto webovej stránke). Poznámka: V polovici osemdesiatych rokov uplynulého storočia vznikla na televíznom vykrývači na Dubníku, na východnom Slovenku, vážna havária. Príčinou nebol ani blesk, ani víchrica, dôvodom havárie bolo neprispôsobenie anténneho systému k napájaču antény, na ktorom vznikla stojatá vlna. Intenzita elektrického poľa v maximách stojatej vlny na napájači prekročila prípustnú hodnotu, v dielektriku napájača vznikli elektrické prierazy a napájač zhorel. V učebnici „Elektronika veľmi vysokých frekvencií“, v kap. 5 je odvodený výraz pre výpočet vlnovej impedancie koaxiálneho vedenia v tvare Zv = U+/I+= E+/H+ = (L/C)1/2 = (Z0/2pi) ln (a/b), kde L je indukčnosť, C je kapacita vedenia na jednotku jeho dĺžky, pi =3,14159..... je Ludolfovo číslo , a je vnútorný polomer plášťa vedenia a b je polomer jeho vnútorného vodiča (obr. 1b), Z0 = 376,73/√er ohmov je vlnová impedancia neohraničeného dielektrika s relatívnou permitivitou er. Predpokladá sa, že vodiče vedenia sú neferomagnetické, teda ich relatívna permeabilita µr = 1 (pozri napr. „Elektromagnetizmus“, kap. 3 a 7). Posledný výraz možno použiť pri výbere parametrov vedenia a/b a permitivity jeho dielektrika er, ak je požadovaná vlnová impedancia vedenia Zv. Naopak, neznáma vlnová impedancia sa zmerá tak, že sa zmerajú indukčnosť L a kapacita C vedenia na jednotku jeho dĺžky napr. rezonančným meračom a impedancia sa vypočíta z hore uvedeného výrazu. Avšak situácia nie je tak jednoduchá, ak zoberieme do úvahy, že reálne káble sú vyrábané z vodičov, ktoré majú konečnú (nie nekonečnú) vodivosť a z dielektrickej výplne, ktorá popri istej permitivite má aj nejaké straty. Tieto straty spôsobujú útlm výkonu aTEM pozdĺž vedenia a tento závisí od pomeru a/b, teda od jeho vlnovej impedancie Zv. Na druhej strane prenášaný elektromagnetický výkon Pmax pozdĺž kábla je určený plochou medzikružia s polomermi a a b, teda pri danom polomere a vedenia závisí tiež od Zv. Nakoniec veľkosť polomeru b pri danom a je limitovaná maximálnou intenzitou elektrického poľa na povrchu vnútorného vodiča, ktorá nesmie presiahnuť istú maximálnu hodnotu Emax, nad ktorou by vo vedení hrozili už spomínané elektrické prierazy (pozri úlohu 39 v učebnici „Elektromagnetizmus“). Závislosti Pmax, Emax a aTEM od Zv sú odvodené v učebnici „Elektronika veľmi vysokých frekvencií“, v kap. 5 a sú tvaru Pmax = AZve-(4piZv/Z0), Emax = Be-(4piZv/Z0)/Zv, aTEM = C[1 + e-(4piZv/Z0)]/Zv,
Obr. 2 kde A, B, C sú pre danú frekvenciu konštanty, e je Eulerovo číslo (základ prirodzených logaritmov). Tieto závislosti sú relatívne zložité a preto sú graficky znázornené na obr. 2 (pre er = 1). Zo týchto závislosti, ktoré sú pôvodné - z literatúry nekopírované - vidieť, že maximálny výkon prenesie vedenie s vlnovou impedanciou Zv = 30 ohmov (a/b = 1,65), minimálny útlm má vedenie s vlnovou impedanciou Zv = 77 ohmov (a/b = 3,61) a minimálna intenzita elektrického poľa na povrchu vnútorného vodiča je vo vedení s vlnovou impedanciou Zv = 60 ohmov (a/b = e = 2,718.....). Pri voľbe rozmerov koaxiálneho vedenia pre žiadanú vlnovú impedanciu treba brať do úvahy niekoľko praktických požiadavok, a to:
a) zabezpečiť požadované frekvenčné (vlnové) pásmo od 0 po fmax,
b) dosiahnuť maximum prenášaného výkonu (Zv = 30 ohmov) ,
c) dosiahnuť minimálny útlm (Zv = 77 ohmov),
d) dosiahnuť minimálnu intenzitu elektrického poľa na povrchu vnútorného vodiča (Zv = 60 ohmov).
Požiadavka a) žiada, aby sa výkon prenášal výkon iba na TEM-vlne. Tu možno splniť, ak polomeru vnútorného vodiča bmax sa vyberie podľa vzťahu bmax ≤ c/[pifmax√er (1 + a/b)], kde fmax je hraničná frekvencia prenášaná na TEM-vlne (pozri „Elektronika veľmi vysokých frekvencií“, výraz (5.17)). Voľba vlnovej impedancie vedení je kompromisom medzi požiadavkami na mechanickú konštrukciu, požiadavky na elektrické vlastnosti a jednoduchú náväznosť na ostatné časti prenosového reťazca. Požiadavky b) až d) sú do istej miery protichodné. Podľa odporúčania Medzinárodnej elektrotechnickej komisie (IEC) sú vo všetkých štátoch (okrem Nemecka) vlnové impedancie koaxiálnych vedení napr. pre anténne napájače normované jednotným spôsobom a to 75 ohmov a v Nemecku 60 ohmov (T. Český: Antény pro příjem televize, SNTL Praha 1987). Takýto výber hodnôt Zv je v súlade s grafmi na obr. 2. Pri voľbe Zv = 75 ohmov z grafov na obr. 2 vidieť, že aTEM a Emax sú takmer minimálne. Pre výkonové vedenia treba Zv voliť ináč, bližšie k hodnote Zv = 30 ohmov, hodnoty aTEM a Emax sa však zhoršujú. Hodnota Zv odporúčaná IEC súvisí s rezonančnou impedanciou polvlnového aj skladaného dipólu, ktoré sú cca 75 ohmov (vo voľnom priestore presne 73,13 ohmov) a 4 × 75 ohmov = 300 ohmov.
Ako sa norma dodržiava v USA, možno najlepšie posúdiť z citátu zo známej mikrovlnárskej učebnice P. Rizzi: Microwave Engineering, Prentice Hall, Englewood Cliffs, New Jersey 07632: „Except for the occasional use of 75 ohm line, coaxial lines and equipment are usually designed for Zv = 50 ohms.“ Želám Vám pekný deň! Autor
17. Aký je rozdiel medzi sériovou a paralelnou rezonanciou v elektrických obvodoch.
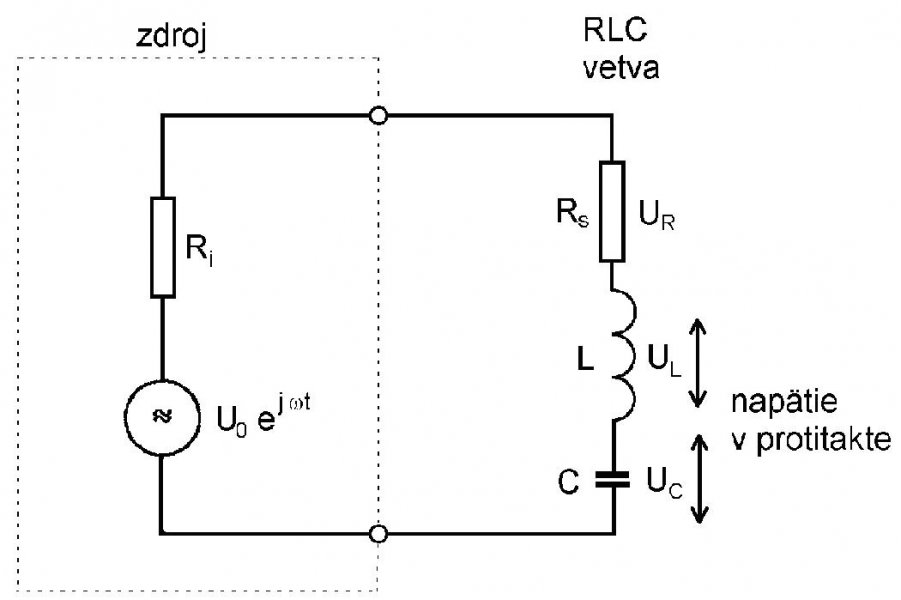
V učebniciach fyziky v časti o elektrických obvodoch sa analyzuje aj rezonančný obvod, presnejšie povedané sériový rezonančný obvod RLC (pozri obr. 1a). Takmer v žiadnej učebnici ale nie je analyzovaný paralelný rezonančný obvod RLC (obr. 2a), ktorý je možno v praxi dôležitejší. Príčina nezáujmu o tento obvod tkvie hlavne v skutočnosti, že jeho analýza je podstatne zložitejšia a pokusy o ňu, sú často chybné. Nemám pritom na mysli analýzy v odborných elektrotechnických monografiach, ale skôr analýzy v učebniciach fyziky, kde by sa mala objasniť fyzikálna podstatu paralelnej rezonancie.
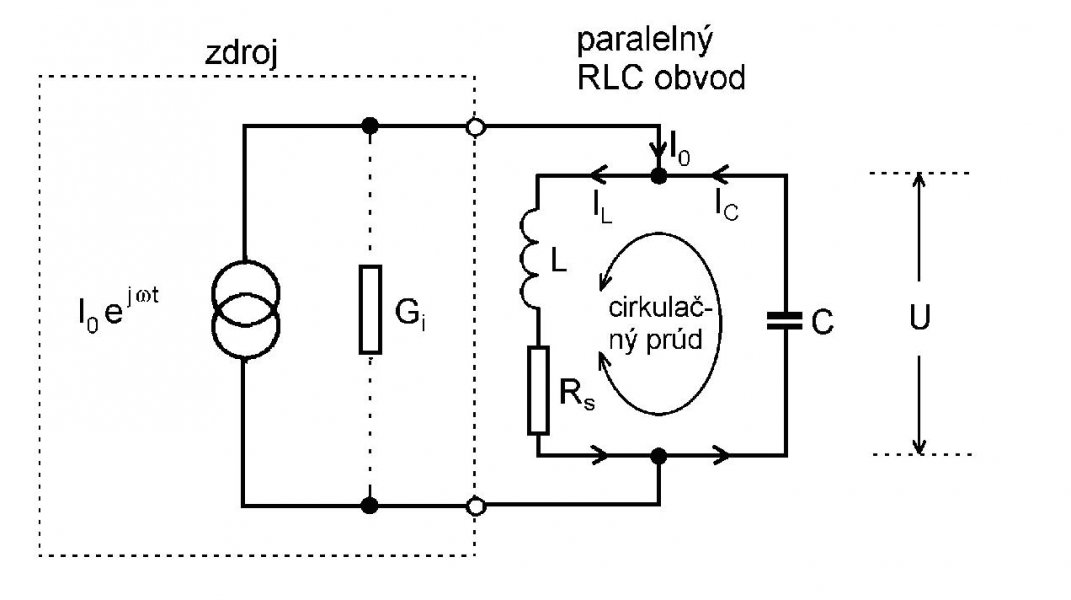
Základná chyba, ktorej sa ľudia vyšetrujúci vlastnosti paralelného obvodu RLC dopúšťaju je, že za paralelný obvod považujú striktné paralelné zapojenie troch prvkov R, L a C, lenže takýto obvod v elektrotechnickej praxi neexistuje a preto jeho analýza nemá žiadny prakticky význam a znamená iba informačný šum. Ak by aj obvod existoval, pre výraznú rezonanciu by odpor R musel byť veľmi veľký, najlepšie nekonečný, ale rozhodne podstatne väčší ako rezonančné reaktancie ideálnej indukčnosti a kapacity. Prakticky paralelný obvod RLC pozostáva z cievka s nenulovým malým sériovým odporom jej drôtu a z kondenzátora so zvodovým, paralelným a veľmi veľkým odporom dielektrika. Skúsenosť ukazuje, že veľký zvodový odpor kondenzátora obyčajne možno zanedbať (považovať ho za nekonečný), ale malý odpor cievky nie a tak praktický paralelný RLC obvod vyzerá ako na obr. 2a.
Obr. 1a Obr.2a
Pojem rezonancia (z lat. resonantia – ozvena) predstavuje fascinujúci fyzikálny jav v systéme, ktorý je schopný harmonických (sínusových) kmitov. Jav sa prejavuje enormným zvýšením amplitúdy kmitov nejakého kmitavého deja pod účinkom periodickej sily, alebo iného periodického účinku. To sa stane pri istej, pre systém charakteristickej frekvencii, ktorú nazývame rezonančnou, alebo vlastnou frekvenciou frez. Mimo tejto frekvencie systém len slabo reaguje na vonkajšie silové, alebo iné podnety. Okrem vynútených kmitov ja rezonančný systém schopný vykonávať aj vlastné tlmené kmity. Rezonančná a vlastná frekvencia systému sú takmer rovnaké.
Druhým parametrom rezonančnému systému je jeho vlastná kvalita Q0 (angl. Q-faktor, quality Q; nem. der Gütefaktor Q, alebo die Güte Q), pozri napr. „Elektromagnetizmus“, odsek 7.9.1, alebo pojednanie „Elektrická rezonancia“ umiestnené v časti „Knihy“ na tejto webovej stránke. Kvalita je bezrozmerný parameter rezonančného systému, úmerný pomeru energie prijatej systémom Wrez za rezonancie k energii, ktorá sa v systéme počas jednej rezonančnej periódy rozptýli (spotrebuje) Wsp = PT (P je stratový výkon a T je perióda kmitov), teda Q0 = 2piWrez/Wsp = 2piWrez/(PT), kde pi = 3,14159..... je Ludolfovo číslo. Čim vyššia je kvalita systému, tým je systém „ochotnejší“ kmitať. V prírode existujú systémy, ktoré sú schopné s vysokou amplitúdou kmitať na vlastnej, alebo rezonančnej frekvencii (napríklad rezonančné obvody, ktoré sa chystáme analyzovať, rôzne druhy kyvadiel, napr. dieťa na hojdačke, alebo ak chcete, rezonancia jadrových magnetických momentov v striedavom magnetickom poli pri jadrovej magnetickej rezonancii, prípadne supravodivé dutinové rezonátory s kvalitou až niekoľko miliónov). Sú to systémy, v ktorých straty energie počas kmitania sú nízke. Naopak, existujú systémy, v ktorých jav rezonancie je škodlivý, až vražedný (napr. kmitanie mrakodrapov, alebo mostov vo víchrici a p.). Tam sa žiada, aby energetické straty systému boli naopak vysoké.
Foucaultovo kyvadlo
Jednoduchým príkladom rezonančného systému z bežného života je dieťa na hojdačke. Ak hojdačka dostane malý počiatočný impulz, dieťa podvedomou zmenou svojho ťažiska v gravitačnom poli Zeme môže rozkmitá hojdačku do veľkých amplitúd. Nepotrebuje k tomu vedieť žiadnu fyziku, musí sa iba hojdať s rezonančnou frekvenciou hojdačky a seba. Na podobnom princípe zmeny polohy ťažiska netlmene kmitá aj špeciálne uspôsobené Foucaultovo kyvadlo, na demonštráciu Coriolisovej sily, umiestnené v rôznych vhodných aj nevhodných inštitúciach. Foucaultovo kyvadlo zavesili komunisti do kupoly Isakievskeho sobora v Petrohrade (vtedy v Leningrade - chrám komunisti vyhlasili za Muzeum ateizmu!) vo výške asi 80 metrov (chrám ma výšku No, ale od našej témy sme sa trochu vzdialili. Vráťme sa k sériovému rezonančnému obvodu, ktorého zapojenie je zobrazené na obr. 1a. Takýto obvod je analyzovaný v stredoškolských učebniciach. K vstupu sériovej vetvy RLC je pripojený napäťový zdroj (generátor) s amplitúdou napätia U0 s premennou frekvenciou f a s nízkym vnútorným odporom Ri (Rs je odpor cievky, ktorý je tiež nízky). Prúd v obvode má priebeh ako na obr.1b. Pri frekvencii nižšej ako frez sa obvod chová ako sériové spojenie odporu a kapacity (kondenzátora), v ktorom prúd predbieha napätie vo fáze (kondenzátor sa musí najprv prúdom nábojov nabiť, aby na ňom vzniklo napätie). Amplitúda prúdu s frekvenciou narastá. Pri rezonančnej frekvencii frez = 1/[2pi(LC)1/2] (známy Thomsonov vzťah) má amplitúda prúdu v obvode maximálnu hodnotu Irez = I0 = U0/R, kde R = Ri + Rs a prúd je vo fáze s napätím zdroja. Napätia na indukčnosti L a kapacite C majú rovnaké amplitúdy, ale sú v protifáze a preto ich súčet UL + UC sa rovná nule. Niekedy sa rezonancia v sériovom obvode nazýva aj napäťová rezonancia – rezonujú napätia na cievke a kondenzátore. Pri frekvencii generátora vyššej ako rezonančná, obvod sa chová ako sériove spojenie odporu a indukčnosti, prúd vo fáze zaostáva za napätím (na indukčnosti vzniká indukované protinapätie, ktoré bráni toku nábojov, teda prúdu). Amplitúda prúdu s frekvenciou klesá. Všetky tieto úvahy možno sledovať graficky na obr. 1b [delta omega = 2pi (f – frez)]. Je otázka, ako sa chová napätie na LC dvojici mimo rezonancie. Na tomto mieste sa dá iba povedať, že na obidvoch stranách rezonančnej frekvencie napätie na LC dvojici dosahuje lokálne maximá s opačnými znamienkami (známa S-krivka). Toto napätie sa žiaľ nedá merať, pretože cievka zahŕňa aj odpor Rs (podrobnejšie v pojednaní „Elektrická rezonancia“ v časti "Knihy"). Nakoniec treba posúdiť kvalitu sériového rezonančného obvodu. Ak straty energie v kondenzátore sú zanedbateľné, potom v obvode sú iba straty v odpore cievky Rs a dá sa ukázať, že vlastná kvalita Q0 je daná výrazom Q0 = 2pifrezL/Rs. Vidíme, že čím menší je odpor cievky, tým vyššia je vlastná kvalita. V praxi dôležitejšia ako vlastná kvalita, je kvalita zaťaženého obvodu Qz. Záťažou pre obvod je odpor generátora Ri, ale aj prípadná iná vonkajšia záťaž. Kvalita zaťaženého obvodu Qzs = 2pifrezL/(Rs + Ri) = Q0/(1 + Ri/Rs). Tento dôležitý výraz svedčí o tom, že ak kvalita zaťaženého obvodu má zostať vysoká, musí byť vnútorný odpor generátora malý, teda najlepšie ak Ri → 0. Takáto, pomerne jednoduchá, je analýza sériového rezonančného obvodu.
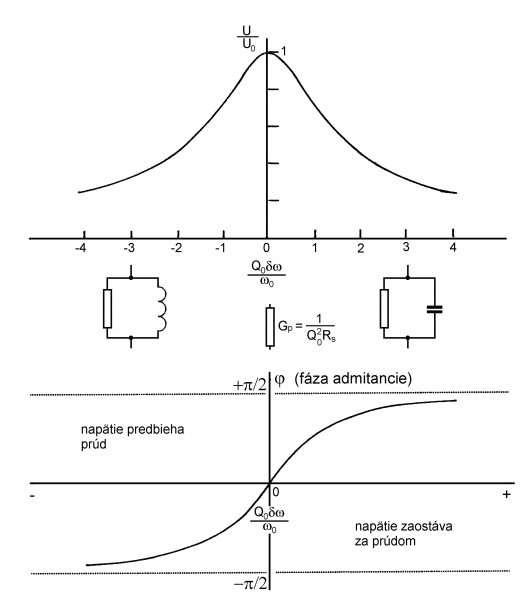
Obr. 1b Obr.2b
*****
Iná je situácia v paralelnom rezonančnom obvode na obr. 2a. Zatiaľ čo sériový rezonančný obvod je za rezonancie nízkoimpedančný, paralelný rezonančný obvod je naopak vysokoimpedančný, o čom sa možno presvedčiť napr. v učebnici „Elektromagnetizmus“, kap. 9, odsek 9.7.2, alebo v pojednaní „Elektrická rezonancia“. Jeho zaťažená kvalita je Qzp = Q0/(1 + Rs/Ri),
a bude tým väčšia, čim vnútorný odpor zdroja (generátora) Ri bude väčší ako Rs (najlepšie ak Ri →). Lenže taký napäťový generátor je vlastne prúdový generátor, ktorého amplitúda prúdu I0 nezávisí (alebo závisí len veľmi málo) od záťaže (pozri obr. 2a). Paralelný rezonančný obvod musí teda vždy napájať prúdový generátor so stálou amplitúdou prúdu I0 a s premennou frekvenciou f. Pri analýze paralelného obvodu spôsobuje ťažkosti sériový odpor Rs cievky (indukčnosti), ktorý síce možno pretransformovať na paralelný, ale taký transformovaný odpor je frekvenčne závislý (pozri pojednanie „Elektrická rezonancia“ v časti "Knihy"). Každý pokus o napájanie paralelného rezonančného obvodu napäťovým generátorom s nízkym vnútorným odporom vedie k záhube obvodu, pretože jeho zaťažená kvalita klesá k nule a obvod nie je schopný kmitov. Poznám učebnicu v ktorej požiadavka vysokého vnútorného odporu zdroja napájajúceho paralelný RLC obvod bola, napriek úprimne mieneným radám, ignorovaná a ako to skončilo, vidieť najlepšie priamo na jej stránkach. V tomto ohľade môže slúžiť ako odstrašujúci príklad. Požiadavka generátora s vysokým výstupným odporom sa ukázala nanajvýš závažná pri praktickom vyšetrovaní vlastností paralelného RLC obvodu v praktiku z elektromagnetizmu. Tvorcovia praktikovej úlohy pri napájaní paralelného RLC obvodu použili bežný RC-generátor s nízky výstupným odporom (niekoľko ohmov), čím zaťaženú kvalitu obvodu mnohonásobne zhodili a obvod stratil rezonančné vlastnosti. Dlho zanovite trvali na správnosti uvedenej teórie v spomínanej učebnici, skúšali využiť katódový sledovač (!) na pripojenie generátora k obvodu, ale úloha už nebola vôbec merateľná, pretože katódový sledovač ešte viac znížuje vnútorný odpor generátora. Až keď si dali povedať a umelo zvýšili výstupný odpor generátora, zaťažená kvalita obvodu stúpla a obvod sa začal správať ako rezonančný.
Vlastnosti paralelného rezonančného obvodu sú podrobne opísané v učebnici "Elektromagnetizmus“, kap. 9, odsek 9.7.2, alebo v pojednaní „Elektrická rezonancia“ v časti "Knihy", tu ich budeme sledovať na obr. 2b. Budeme predpokladať, že odpor cievky je malý, taký že Rs « 2pifrezL = XLrez, čo je rezonančná reaktancia indukčnosti. Admitancia Y na svorkách obvodu so zvyšovaním frekvencie klesá, a minimálna je pri frekvencii frez, kedy má reálnu hodnotu Yrez = 1/(Q02Rs) = Gp (Q0 = 2pifrezL/Rs je už spomínaná vlastná kvalita RLC obvodu a Gp je jeho rezonančná vodivosť). Na obvode je vtedy maximálna amplitúda napätia s hodnotou Urez = U0 = I0/Yrez = Q02RsI0. Ak sa frekvencia generátora bude od nuly zväčšovať, bude sa zväčšovať aj amplitúda cirkulačného prúdu v uzavretom RLC obvode a pri frekvencii f = frez dosiahne maximálnu hodnotu (pozri „Elektromagnetizmus“, kap. 9, odsek 9.7.2) Irez = BCrezUrez = BLrezUrez = Q0I0, kde BCrez ≈ BLrez sú hodnoty rezonančných susceptancii kapacity a indukčnosti. Amplitúda cirkulačného prúdu v RCL obvode v rezonancii Irez je teda Q0-krát väčšia ako amplitúda prúdového generátora I0, preto sa táto rezonancia nazýva prúdovou rezonanciou. Pri frekvenciách nižších ako frez, obvod sa chová ako paralelné spojenie odporu a indukčnosti, napätie na obvode predbieha vo fáze cirkulujúci prúd v obvode a amplitúda napätia na obvode, aj amplitúda cirkulačného prúdu s frekvenciou narastajú. Pri frekvenciách vyšších ako frez, obvod sa chová ako paralelné spojenie odporu a kapacity, napätie na obvode zaostáva vo fáze za prúdom. Nad rezonančnou hodnotou amplitúda napätia na obvode, aj amplitúda cirkulačného prúdu s frekvenciou klesajú k nule. Tak ako paralelný obvod nemôže byť napájaný z napäťového zdroja, ani sériový obvod nemôže byť napájaný z prúdového zdroja (z napäťového zdroja s vysokým vnútorným odporom). V takom prípade na svorkách prúdového zdroje pri rezonančnej frekvencii by iba málo pokleslo napätie, pretože sériová RLC vetva má vtedy minimálnu impedanciu. Tých čitateľov, ktorých problematika rezonancie v elektrických obvodoch zaujíma podrobnejšie, odporúčam na kapitolu 9, alebo aspoň odsek 9.7 v učebnici „Elektromagnetizmus“. Možno tiež využiť samostatné pojednanie „Elektrická rezonancia“ umiestnené v časti „Knihy“ na tejto webovej stránke.
Možno povedať, že rezonancia je fascinujúci fyzikálny jav. V telekomunikačnej elektronike, určenej na prenos digitálnych dát význam rezonančných obvodov trochu poklesol, ale vo fyzikálnych laboratóriách a hlavne v prírode rezonancia zostáva stále jedným z najpozoruhodnejších fyzikálnych fenoménov. Želám Vám pekný a úspešný deň! Autor
7.10.2008 18. Čím sa líši prenos elektromagnetickej energie mikrovlnovými obvodmi od prenosu nízkofrekvenčnými obvodmi Aj keď fyzikálna podstata prenosu elektromagnetickej energie nezávisí od frekvencie, spôsob prenosu v rôznych frekvenčných pásmach je rôzny. Pri nízkych frekvenciách sa elektromagnetická energia takmer výlučne prenáša pomocou dvoj- alebo viacvodičových systémov, a elektronické zariadenia môžu obsahovať rôzne elektrotechnické sústredené prvky, ako sú odpory (rezistory R), kondenzátory (kapacity C) a cievky (indukčnosti L), prípadne vzájomné indukčnosti M. Pri nízkych frekvenciách sa obvody zostavené s prvkov R, C, L, M sa nazývajú aj obvody so sústredenými parametrami, pretože každý prvok má svoje presne miesto v obvode. Okrem toho pri nízkych frekvenciach sa tieto prvky považujú za konštantné (hoci to v skutočnosti nie je celkom pravda). Pri jednosmernom, konštantnom napätí a prúde má odpor význam užitočného, alebo neužitočného spotrebiča elektrickej energie, ktorá sa v ňom mení na teplo. Kondenzátor a cievka sú zásobníky elektrickej a magnetickej energie. S prúdom a napätím sú bezprostredne spojené ich elektrické a magnetické polia, ktoré jednoznačne súvisia s prenášanou energiou. Pre opis prenosu energie pri nízkych frekvenciách sa však polia nehodia a to jednak pre ich obťažne merania, ako aj pre ich priestorovú nejednoznačnosť - jednoducho pre ich nepraktičnosť. Dôležitá vlastnosť nízkofrekvenčných obvodov je aj to, že elektrické rozruchy v nich nemajú vlnový charakter, sú iba funkciou frekvencie (amplitúdy veličín na homogénnych úsekoch vodičov nie sú závislé od polohy). Problémy ktoré vznikajú pri prenose elektromagnetických signálov na veľmi vysokých frekvenciách, alebo na mikrovlnách, súvisia s rozptylom energie do okolia netienených vodičov a stratami energie vo vodičoch a dielektrikách. Prenosovými médiami pre mikrovlny môže byť voľný priestor (vákuum) a bezstratové, resp. nízkostratové dielektrika. Elektromagnetický výkon sa môže smerovými, parabolickými anténami v úzkych zväzkoch účinne prenášať z miesta na miesto, čo nie je možné na nízkych frekvenciách. Účinnejšie, ale drahšie sú prenosové vedenia, také ako sú symetrické dvojvodičové vedenia, koaxiálne a páskové vedenia a trubicové vlnovody (pravouhlý a cylindrický). Teória prenosu a spracovania signálov v mikrovlnovej oblasti bude iná, ako teória prenosu elektrickej energie dvoma ľubovoľne „pohodenými“ prúdovodičmi pri nulových, alebo nízkych frekvenciách. Druhá otázka je frekvenčné pásmo mikrovĺn. Je ťažko jednoznačne povedať, kde leží hranica medzi nízkymi (striedavými) a vysokými resp. veľmi vysokými (mikrovlnovými) frekvenciami signálov, pretože ona vlastne neexistuje. Za dolnú frekvenčnú hranicu mikrovĺn sa považuje hranica cca 300 MHz a horná hranica cca 1000 GHz (1GHz = 109 Hz). S praktických dôvodov je elektromagnetické spektrum mikrovĺn rozdelené do viacero pásiem: sú to decimetrové, centimetrové, milimetrové, prípadne submilimetrové pásmo vĺn. So zvyšovaním frekvencie f vlnová dĺžka lambda klesá. Decimetrovým vlnám odpovedajú frekvencie rádovo gigahertz (GHz), centimetrovým vlnám desiatky GHz, tak ako to plynie zo vzťahu f = vf/lambda,
kde vf je fázová rýchlosť vlny (alebo pre harmonické vlny jednoducho rýchlosť vlny). Vo voľnom priestore je táto rýchlosť známa ako rýchlosť svetla c = 299 792 458 m/s. Uvedený vzťah má potom tvar f = c/lambda0. Dĺžka vlny lambda0 vo voľnom priestore je vždy väčšia ako vlnová dĺžka lambda v ľubovoľnom látkovom prostredí pri tej istej frekvencii (lambda0 > lambda) a teda rýchlosť vlny vf je vždy menšia ako rýchlosť svetla c, ktorá je limitnou maximálnou rýchlosťou, ktorou sa môžu pohybujú hmotné objekty a šíriť elektromagnetické vlny v prírode.
Pre mikrovlny existujú tri dôležité charakteristiky, ktoré ich odlišujú na jednej strane od signálov nízkych frekvencií a na druhej strane od optických frekvencií.
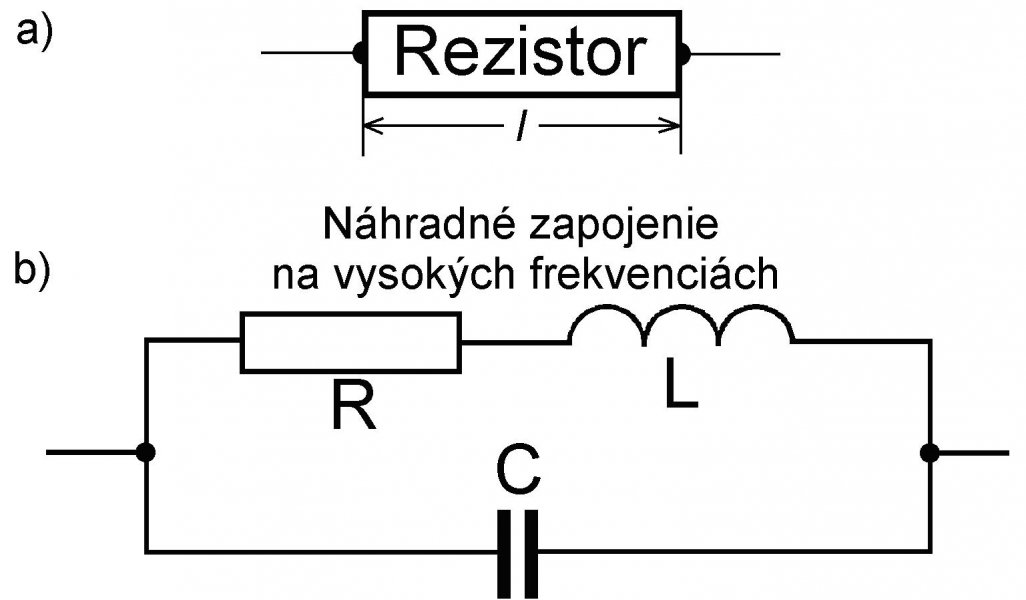
Obr. 1: Rezistor a jeho vysokofrekvenčná náhrada Za prvé, fyzická veľkosť väčšiny mikrovlnových prvkov a obvodov je porovnateľná s operačnou vlnovou dĺžkou. Nie je to tak v prípade optických, alebo nízkofrekvenčných zariadení. Pri optických frekvenciách rozmernosť používaných zariadení ako sú šošovky, objektívy a zrkadlá sú oveľa väčšia ako vlnová dĺžka svetla. Na druhej strane v striedavých elektrických obvodoch sú rozmery elektrotechnických prvkov oveľa menšie ako sú odpovedajúce vlnové dĺžky. Ako príklad môže slúžiť bežný rezistor – odporový valček dĺžky l s dvoma prívodmi (pozri obr. 1a). Striedavý sinusoidálný prúd, ktorý vstupuje do valčeka jedným koncom sa len veľmi málo líši od prúdu, ktorý na druhom konci z neho vyteká. Tento malý rozdiel možno vyjadriť ako malý rozdiel fáze prúdu, alebo malý časový posuv ts prúdu na sinusoide. Časový posuv ts je pri nízkych frekvenciách zanedbateľný v porovnaní s periódou T striedavého signálu. Matematicky vyjadrené, platí: ts = l/vf « T = 1/f = lambda/vf z čoho plynie, že dĺžka rezistora l « lambda. Inými slovami povedané, striedavé siete a prvky z ktorých sú zostavené majú rozmery, ktoré sú oproti vlnovej dĺžke zanedbateľné. Na rozdiel od nízkych frekvencií, na mikrovlnách prvky treba považovať za rozložené (napr. na mikrovlnových vedeniach) a obvody sa nazývajú obvody s rozloženými parametrami. So stúpajúcou frekvenciou sa pojem prvku v obvode úplne stráca. Tak je to napr. v dutinových rezonátoroch, kde pojmy ako je odpor, kapacita a indukčnosť nemajú zmysel. V texte sa tiež používa relatívny pojem dlhé prenosové vedenie - sú to vedenia, ktorých dĺžka je väčšia ako dĺžka jednej štvrťvlny. Skutočnosť, že rozmery prvkov v mikrovlnovej oblasti sú porovnateľné s vlnovou dĺžkou nie je jediná, ktorú treba brať do úvahy. Napríklad pre navrhovateľa nízkofrekvenčného obvodu uhlíkový rezistor predstavuje čistú rezistanciu (odpor R). Pre navrhovateľa mikrovlnového obvodu predstavuje rezistor odpor R, súčasne aj paralelne pripojený kondenzátor C, ktorý tvoria prívody a izolačná vrstva na povrchu rezistora. Prívody samotné sú sériové indukčnosti L s odporom (pozri obr. 1b). Aké veľké sú reaktancie príslušných prvkov, to závisí od frekvencie, ale v mnohých prípadoch reaktancie spojené s uvedenými indukčnosťami a kapacitou robia také rezistory v mikrovlnej oblasti nepoužiteľné. V špeciálne navrhovaných rezistoroch určených pre mikrovlnovú oblasť sú tieto reaktancie minimalizované. Druhým javom, ktorý si vyžaduje pozornosť inžinierov-mikrovlnárov je skinefekt – jav ktorý sa prejavuje zhoršeným prenikaním elektromagnetických polí, prúdov a napätí do vnútra vodivých materiálov pri zvyšovaní frekvencie prúdu a napätia. Tak napríklad pri frekvencii 1000 MHz je hĺbka prieniku poľa do medi iba niekoľko mikrometrov. Dôsledkom je, že mikrovlnové prúdy tečú iba po povrchu vodiča, čo dramaticky zvyšuje odpor používaných vodičov.Táto skutočnosť súčasne vysvetľuje, prečo vysoké vysokofrekvenčné napätie neohrozuje človeka, ktorý sa ocitne v jeho dosahu. Prúdy napr. Teslovho transformátora, pri rôznych elektrických show, tečú iba po povrchu ľudského tela a neprenikajú do životne dôležitých orgánov. Na mikrovlnách treba preto prijímať opatrenia na minimalizovanie obvodových odporov napríklad striebrením, prípadne leštením vodivých povrchov.
Treťou osobitou charakteristikou mikrovlnových obvodov je používaná meracia technika. Na nízkych frekvenciách vlastnosti obvodov a systémov sú určene meraním napätí a prúdov, pre ktoré boli vypracované množstvá metód. V oblasti veľmi vysokých frekvencií je tento prístup v obmedzenej miere možný na dvojvodičových vedeniach pracujúcich na transverzálne-elektromagnetických (TEM) vlnách, avšak nie je možný na vlnách vyšších typov (transverzálne-elektrické TE (H), alebo transverzálne-magnetické TM (E) vlnách) v trubicových vlnovodoch (pravouhlý, cylindrický vlnovod a i.). Tam takýto prístup úplne zlyháva, pretože mikrovlnové napätia a prúdy sú nejednoznačné a nemusia mať smer prenosu energie (Poyntingovho vektora). Tam treba merať polia a impedancie, alebo priamo merať mikrovlnový výkon, alebo tok Poyntingovho vektora (pozri učebnicu „Elektronika veľmi vysokých frekvencií“ na tejto webovej stránke).
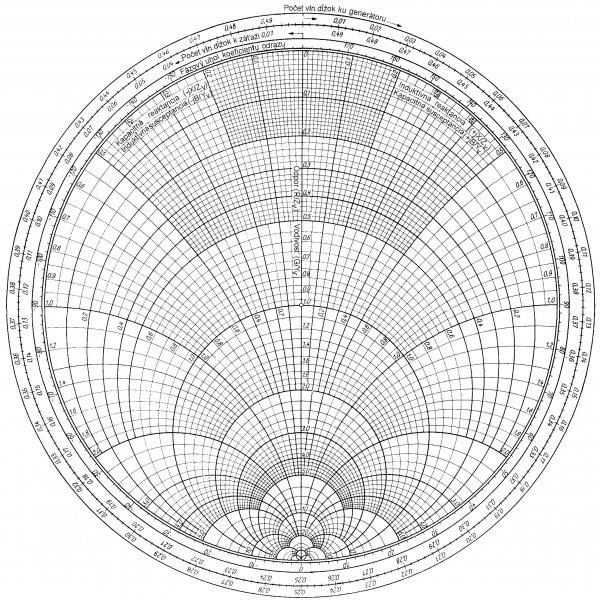
Pri riešení mnohých praktických problémov mikrovlnovej elektroniky sa s výhodou používa grafická pomôcka, ktorá sa nazýva kruhový impedančný (admitančný) diagram, alebo podľa jeho pôvodcu Smithov diagram. Tento geniálny diagram vymyslel americký elektrotechnik Phillip H. Smith (1905 – 1987) v roku 1937-39, teda tesne pred vypuknutím druhej svetovej vojny. Aj tento elegantne vyzerajúci diagram mal svoj podiel na porážke nemeckej Luftwaffe v bitke o Britániu.
Obr. 2: Kruhový impedančný (admitančný) diagram
(Smithov diagram)
Kruhový diagram popri svojej bizarnej kráse (obr. 2) pomáha riešiť množstvo praktických úloh spojených s prenosovými vedeniami, filtrami, rezonátormi, oscilátormi a i. Na vedeniach sú to predovšetkým výpočet a transformácie impedancií (resp. admitancií), výpočet koeficientu odrazu a pomeru stojatých vĺn (PSV), prispôsobovanie impedancií, na rezonátoroch je to meranie ich kvality a mnohé iné (uvedené pojmy možno nájsť v učebnici „Elektronika veľmi vysokých frekvencii“). Aj keď tieto úlohy sú dnes riešiteľné na počítači, výhodou diagramu je, že dáva možnosť vytvárať stratégiu postupov a tak umožňuje vidieť riešenia priam ako na dlani. Pracovná verzia Smithovho diagramu je uvedená na obr. 2. V učebniciach „Elektronika veľmi vysokých frekvencií“ a v zborníku „Úlohy k mikrovlnovým vedeniam a rezonátorov“ na tejto webovej stránke nájdete kompletnú teóriu Smithovho diagramu a množstvo príkladov na jeho priame numerické použitie, aké bežne v učebniciach nenájdete. Smithov diagramu je pracovný prostriedok mikrovlnovej techniky, ale dá sa použiť napríklad aj v akustike. Na nízkych frekvenciách diagram nemá použitie - chyba tu vlnová závislosť veličín. Už v časoch mojich štúdií som bol týmto diagramom fascinovaný.
Obr. 3: HP analyzátor obvodov (HP network analyzer)
so Smithovym diagramom
*****
Rovnako som bol fascinovaný jednoduchým, až triviálnym dvojvodičovým vedením, známym pod názvom štvrťvlnové vedenie, alebo štvrťvlnový transformátor. Tu treba pripomenúť, že na dlhých vedeniach a vo vlnovodoch sa ich impedancia na polvlnových dĺžkach periodicky opakuje (pozri učebnicu „Elektronika veľmi vysokých frekvencií“). Štvrťvlnový transformátor fyzicky predstavuje kúsok dvojvodičového symetrického, alebo koaxiálneho vedenia, prípadne trubicového vlnovodu (pozri obr. 4a). Toto vedenie pri danej frekvencii a odpovedajúcej štvrťvlnovej dĺžke inverzne transformuje impedanciu Zvýst z výstupu na jeho vstup Zvst a naopak, podľa vzťahu Zvst = Zv2/Zvýst (kde Zv je reálna vlnová impedancia vedenia – pozri úvahu 16). Vstupná a výstupná impedancia môžu byť komplexné, alebo rezistívne. Tak napríklad, ak výstupná impedancia je nulová (skratovaný koniec vedenia), potom vstupná impedancia je nekonečná (otvorený vstup vedenia) a naopak.
Už len tento prípad inverznej transformácie umožňuje jeho zaujímavé využitia. Napríklad pri danej frekvencii na konci otvorené štvrťvlnové vedenie má na vstupe vlastnosti skratu, ale súčasne, ak má vedenie určité straty (a tie vždy nejaké má), potom predstavuje na vstupe malý odpor a v okolí tejto frekvencie predstavuje reálny sériový rezonančný obvod. Na druhej strane, ak vedenie je na výstupe skratované, jeho vstupná impedancia je nekonečná (alebo pre reálne vedenie iba veľmi veľká), v okolí danej frekvencie sa chová ako paralelný rezonančný obvod. Vlastnosť nekonečnej vstupnej impedancie vedenia predurčuje použitie štvrťvlnového vedenia ako štvrťvlnového izolátora a pri danej frekvencii môže slúžiť ako mechanická opora (stožiar) pre iné vedenia, alebo napríklad ako elektricky neaktívny držiak dipólovej antény (žiaľ presne iba pri jednej frekvencii).
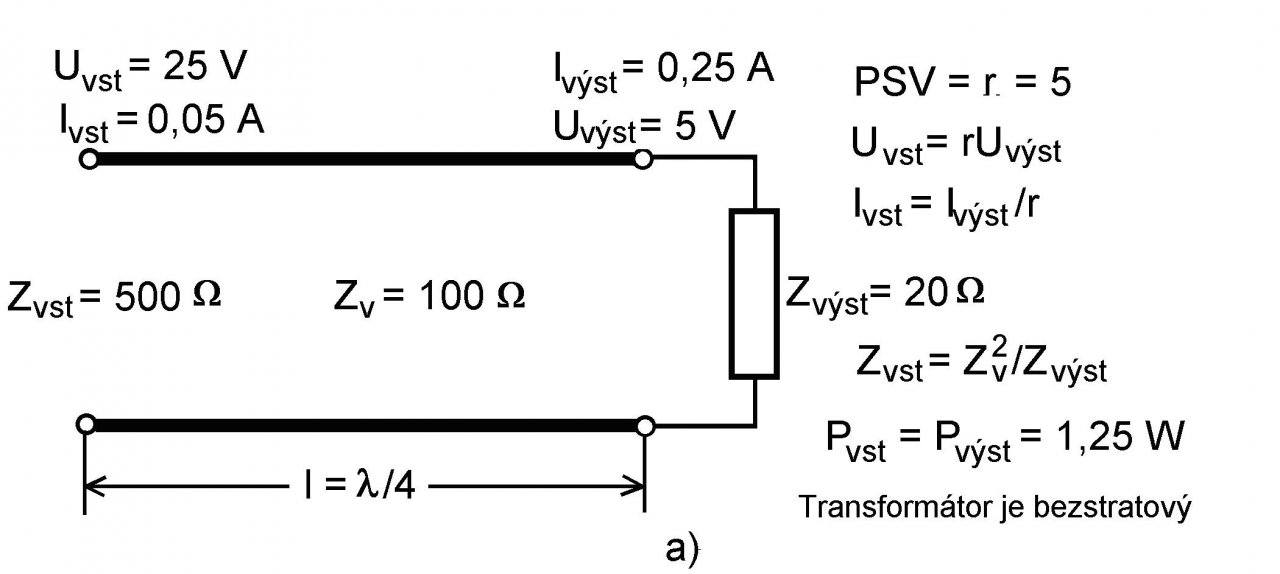 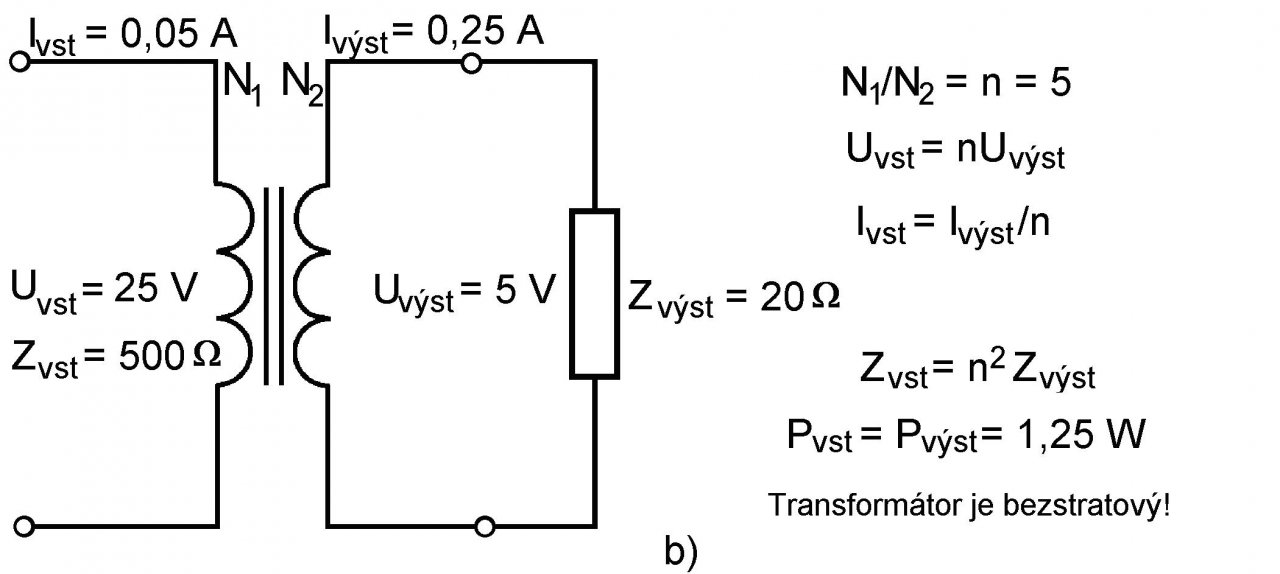
Ak na výstupe štvrťvlnového bezstratového vedenia je pripojená odporová záťaž Zvýst < Zv (pozri obr. 4a), potom vstupná, čisté odporová impedancia vedenia je Zvst > Zv. V prípade, ak ku vstupu je pripojený napäťový generátor s amplitúdou Uvst (predpokladá sa, že je neprispôsobený), potom na vedení vznikne štvrťvlnová napäťová stojatá vlna s maximom amplitúdy napätia Umax = Uvst na vstupe vedenia a s minimom amplitúdy napätia Umin = Uvýst na záťaži. Pomer týchto napätí sa rovná pomeru stojatých vĺn PSV, teda Umax/Umin = Uvst/Uvýst = PSV = r a súčasne platí, že Zvst/Zvýst = r2. Rovnaké vlastnosti má na nízkych frekvenciách obyčajný napäťovo-prúdový transformátor so zostupným pomerom počtu závitov N1/N2 = n > 1, alebo N1 > N2 (od primáru na sekundár), navinutých na feromagnetickom, alebo feritovom jadre (obr. 4b). Ekvivalentom PSV = r v nf transformátore je pomer počtu závitov N1/N2 = n. Rozdiel medzi transformátormi je ten, že zatiaľ čo nízkofrekvenčný je v širokom rozsahu frekvencii frekvenčne nezávislý, mikrovlnový presne platí iba pre jednú frekvenciu a približne v jej malom okolí. Tí, ktorí poznajú štruktúru a konštrukciu nf transformátora môžu oceniť jeho jednoduchý ekvivalent na mikrovlnových frekvenciách. Možno sa takisto presvedčiť, že ak Zvýst > Zv, potom sa jedná o štvrťvlnový transformátor ekvivalentný nf transformátoru so vzostupným prevodom smerom k záťaži, pre ktorý n < 1, alebo N1 < N2. Aj pre uvedené vlastnosti sa dané vedenie nazýva štvrťvlnový transformátor. Najväčšie využitie má však štvrťvlnové vedenie v prispôsobovacej technike. Ak sa štvrťvlnové vedenie zaradí medzi záťaž Zz a vstupné vedenie s vlnovou impedanciou Zv rôznej od Zz, potom vhodnou voľbou vlnovej impedancie štvrťvlnového vedenia Z0v = (ZvZz)1/2 možno dosiahnúť prispôsobenie. Toto sú iba niektoré využitia tohto čarovného a pritom tak jednoduchého vedenia. V úvahe som uviedol iba niektoré aspekty prenosu a spracovania elektromagnetickej energie na mikrovlnách. Vidíme, že technicky sa prenos elektromagnetickej energie značne líši od prenosu na nízkych frekvenciách, hoci jeho fyzikálna povaha je rovnaká. Prajem vám pekný a príjemný deň! Autor 15.10.2008
19. Niekoľko úloh s kondenzátormi!
V úvahe 10 sme analyzovali spôsoby riešenia kapacitných sieti s rozpakmi a s nevyslovenou otázkou, či niekto môže mať potrebu analyzovať takéto siete. Tu by som chcel ukázať, že takéto prakticky potrebné siete existujú, sú užitočné a pritom môžu byť veľmi zaujímavé. Ako príklad kapacitných sieti možno uviesť rôzne kapacitné mostíky, fázové posúvače, bezstratové kapacitné deliče a i. Také siete sú obzvlášť užitočné pri použití striedavých napätí, kde kapacity vystupujú ako kapacitné susceptancie, alebo reaktancie. Považujem za dlh voči mojim čitateľom, uviesť nejaký príklad na použitie pravidiel z úvahy 10.
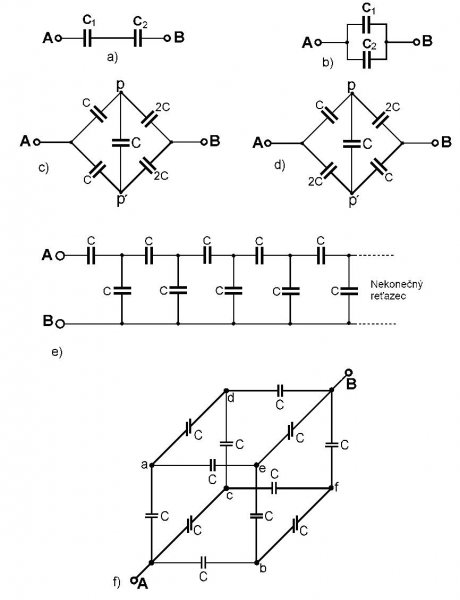
Obr. 1
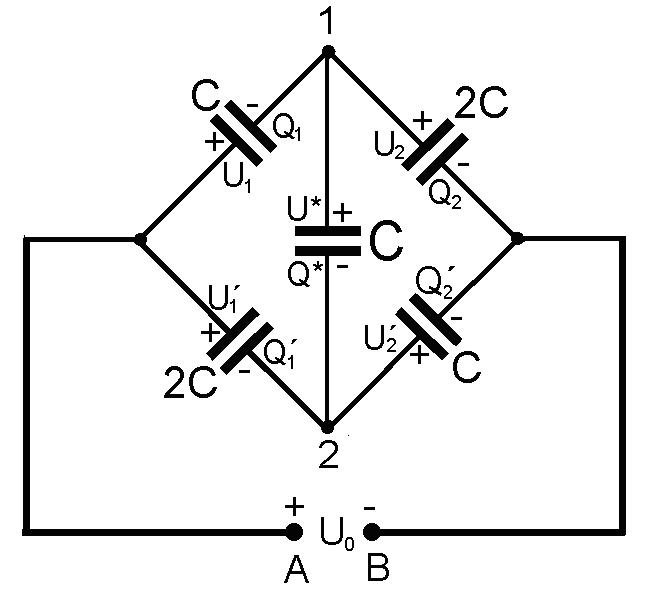
Na obr. 1 je šesť sieti zostavených z kondenzátorov. Vo všetkých šiestich prípadoch treba určiť kapacitu medzi svorkami A-B. Možno k tomu využiť výsledky analýzy z úvahy 10, ale v niektorých z úloh je jednoduchšie využiť isté symetrie, odporúčané v úvahe 15. ***** Zapojenia a) a b) sú známe zo strednej školy a preto sa nimi nebudeme zaoberať. V prípade a) výsledná kapacita je Cvýsl = C1C2/(C1 + C2) a v prípade b) Cvýsl = C1 + C2. ***** V prípade kapacitného mostu podľa obrázka c) by sa dala využiť analýza z úvahy 10 s využitím výrazov (1) a (2), ale tu si možno všimnúť, že zapojenie je symetrické okolo spojnice svoriek A a B. Ak sa ku svorkám A a B pripojí napäťový zdroj, body P a P´ budú na rovnakom potenciále, možno ich teda pre účely analýzy skratovať, alebo aj neskratovať – priečny kondenzátor sa pri analýze neuplatní. Výsledok je naporúdzi okamžite Cvýsl = (4/3)C.
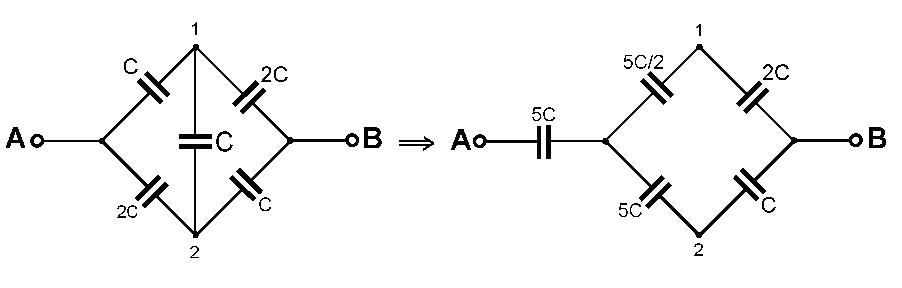
O takom moste hovoríme, že je vyvážený. ***** Kapacitný most na obrázku d) sa dá analyzovať napríklad využitím transformácie kapacitného trojuholníka na kapacitnú hviezdu (pozri "Elektromagnetizmus", úlohu 60). Takáto transformácia je urobená na obr. 4a. Pri transformácii most prešiel na obyčajné sériovo-paralelné zapojenie kondenzátorov, a jeho výsledná kapacita medzi svorkami A-B je Cvýsl = (7/5)C.
Obr. 4a
Na moste podľa obrázku d) budeme demonštrovať aj použitie analýzy z úvahy
Obr. 4b
Na obr. 4b je dotyčný most pripojený k zdroju elektromotorického napätia U0. Zostavíme systém piatich rovníc pre päť neznámych napätí. Pre elektródy spojené v uzloch 1 a 2 platia rovnice podľa (1) úvahy 10 – CU1 + 2CU2 + CU* = 0, – 2CU1´ + CU2´ – CU* = 0. Pre vonkajší obvod mostu platí rovnica podľa (2) U1 + U2 = U0 a pre dve vnútorné slučky mosta rovnice U1 + U* – U1´ = 0, U2 – U2´ – U*= 0. Systém týchto päť rovníc pre neznáme napätia U1, U2, U1´, U2´ a U* dáva možnosť nájsť dve potrebné napätia a to
U1 = 3U0/5 = Q1/C a U1´ = 2U0/5 = Q1´/( alebo
Q1 = 3U0C/5 a Q1´ = 4U0C/5.
Kapacita medzi svorkami A a B je daná výrazom
Cvýsl = (Q1 + Q1´)/U0 = (7/5)C
Skutočná výhody pravidiel z úvahy 10 by sa ale ukázala až v prípade, keby všetky kondenzátory boli rôzne.
***** Nekonečný reťazec na obrázku e) má tú vlastnosť, že jeho vstupná kapacita sa nezmení, ak sa na jeho vstup pridá ďalšia sériovo-paralelná bunka C-C, ako je to ukázané na obr. 5. Pre vstupnú kapacitu platí rovnica
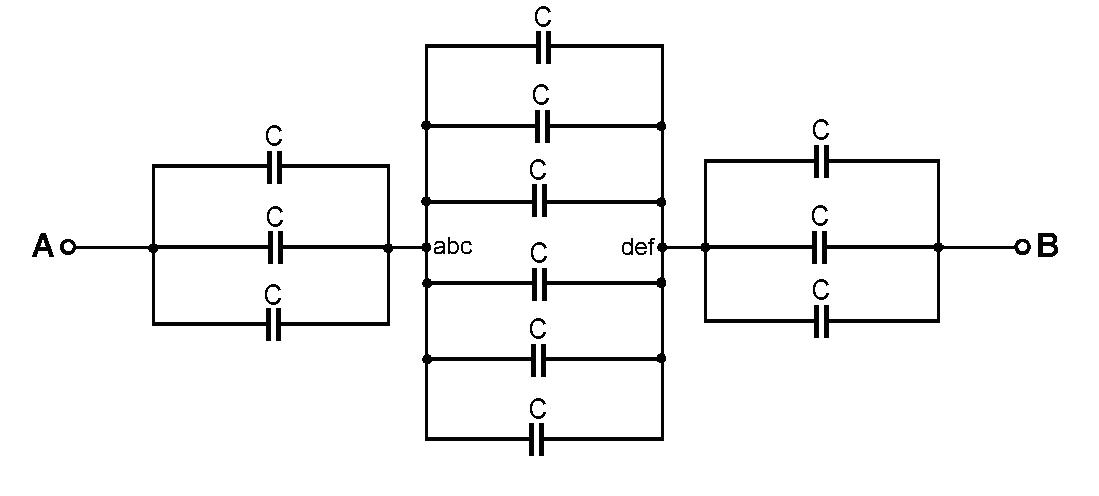
Obr. 5 1/Cvýsl = 1/C + (C + Cvýsl)/(CCvýsl) a po úprave C2výsl + CCvýsl – C2 = 0. Je to kvadratická rovnica, ktorej kladný koreň je hľadané riešenie Cvýsl = (1/2)(√5 -1)C ≈ 0,618C. ***** Zapojenie na obrázku f) vyzerá veľmi zložito – je to kocka, ktorej hrany tvoria 12 rovnakých kondenzátorov C. Aj tu si možno všimnúť isté symetrie. Vidieť, že vrcholy kocky abc musia byť na rovnakých potenciáloch, možno ich teda pre účely analýzy skratovať. To isté platy pre vrcholy def – aj tieto vrcholy možno skratovať. Po tejto úprave vznikne zapojenie na obr. 6. Z neho bezprostredne vidieť, že Cvýsl = (6/5)C. Analýza pomocou pravidiel (1) a (2) úvahy 10 by vyžadovala zostaviť a riešiť 12 nezávislých algebrických rovníc.
Obr. 6 ***** A nakoniec jeden problém na "domácu úlohu". V priestore je umiestnených n bodov (uzlov), pričom každý s každým je spojený jedným kondenzátorom s kapacitou C. Vypočítajte výslednú kapacitu Cvýsl medzi dvoma uzlami. Výsledok je jednoduchý Cvýsl = (n/2)C. Pre zaujímavosť - ak by bolo n = 10, sieť by obsahovala 45 kondenzátorov a ak kapacita jedného kondenzátora by bola C = 1 µF, potom Cvýsl = 5 µF. Šestnásť kondenzátorov by bolo pod napätím, zvyšné dvadsaťdeväť kondenzátory by boli nenabité. Podobná úloha je riešená v učebnici "Elektromagnetizmus", ale pre odporovú sieť. Želám Vám pekný deň! Autor 25.10.2008 20. Ako vysoko nad povrchom Zeme musia „visieť“ geostacionárne družice?
Aj keď táto úvaha tematicky do súboru mojich úvah nepatri, pretože je to problematika nebeskej mechaniky, myslím že z fyzikálneho hľadiska doplňuje úvahy o prenose a spracovaní elektromagnetických signálov aj pomocou umelých družíc Zeme.
Obr. 1: Arthur C. Clarke
(16.12.1917 – 19.3.2008)
Vyslanie geostacionárnych družíc, dokonca vytvorenie celého družicového komunikačného systému predpovedal už v roku 1945 americký scifi spisovateľ a vedec, autor fascinujúcej „Vesmírnej odysey“ Arthur C. Clarke, ktorý odhadol, že celu zemeguľu, s výnimkou zemských pólov, možno elektromagnetickými signálmi pokryť pomocou vysielačov na troch geostacionárnych družiciach, ktoré sa niekedy nazývajú aj Clarkove družice.
Podľa názvu geostacionárne sú družice, ktoré vzhľadom k Zemi udržiavajú stabilnú polohu nad jej povrchom. Geostacionárne polohy družíc existujú iba v rovníkovej rovine, v ktorej sa družice pohybujú okolo polárnej osi synchrónne, východným smerom, s periódou 24-hodinového obehu okolo zemegule. Z hľadiska pozorovateľa spojeného so Zemou družice „visia“ nad jedným bodom zemského rovníka. Uhlová rýchlosť družice okolo Zeme sa musí rovnať uhlovej rýchlosti otáčania zemegule a to je možné iba pri jedinej výške družice nad zemským povrchom. Kladieme si za úlohu určiť túto výšku a tiež obežnú rýchlosť družice na jej dráhe.  Obr. 2: Telekomunikačná družica
Pri výpočte potrebnej výšky družice sa vychádza zo zákona všeobecnej gravitácie. Podľa neho sila F, ktorou Zem pôsobí na družicu (a naopak) je úmerná súčinu hmotnosti Zeme Mz = 5,98.1024 kg a hmotnosti družice Md a nepriamo úmerná kvadrátu vzdialenosti stredov Rd týchto hmotnosti, teda F = GMdMz/Rd2 = Md×GMz/Rd2 = Md×g(Rd),
kde G = 6,6720×10- g(Rd) = GMz/Rd2 = 4×1014/Rd2 m/s2
je gravitačné zrýchlenie, udeľované družici uloženej vo výške Rd nad stredom Zeme. Toto zrýchlenie sa rovná dostredivému zrýchleniu
g(Rd) = w2×Rd = (4pi2/T2)×Rd m/s2 = 5,2885×10-9Rd m/s2
družice pohybujúcej sa na kruhovej dráhe uhlovou rýchlosťou (pi = 3,14159..... je Ludolfovo číslo)
w = 2pi/T = 7,272×10-5 rad/s, kde T = 24×60×60 s = 86400 s
je perióda otáčania Zeme okolo svojej rotačnej osi (pozri obr. 3) a súčasne perióda obehu družice okolo Zeme.
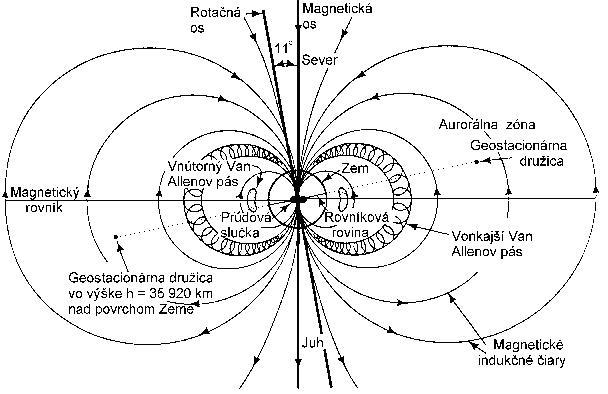
Obr. 3: Schematické zobrazenie zemegule a jej blízkeho vesmírneho okolia
Poznámka k obr. 3: Van Allenove pásy sú radiačné pásy elektrónov a protónov: vnútorný vo výške 1 000 – Porovnaním výrazov pre zrýchlenia g(Rd) dostaneme vzdialenosť družice od stredu Zeme
Rd = (GMz/w2)(1/3) = a pre výšku družice h nad povrchom Zeme (na ktorej sa družica udržuje nad pevným bodom povrchu Zeme) dostávame hodnotu
h = Rd - Rz = (42 290 – 6 370) km =
kde Rz = v = w×(GMz/w2)(1/3) = (GMzw)(1/3) = 3 076 m/s a obehne zemeguľu za čas t = 2piRd/v = T = 24 hodín t.j. za jeden pozemský deň. Samozrejme pozorovateľ zviazaný s povrchom Zeme žiadny pohyb družice nepozoruje. *****
Družice určené pre geostacionárnu dráhu sú obrovské a zložité prístroje, často riadené tými najvýkonnejšími dostupnými procesormi. Päťtonové družice v cenách stoviek miliónov dolárov nie sú dnes vôbec výnimkou. Ich umiestnenie na geostacionárnej dráhe umožní každej družici pokryť viac ako 1/3 zemského povrchu v istom páse okolo rovníka. Družicové telekomunikačné služby sú poskytované na mikrovlnových frekvenciách v pásme od 3 do 30 GHz. Týmto frekvenciám odpovedajú vlnové dĺžky od 10 do Geostacionárna dráha má tri veľké nedostatky. Prvým nedostatkom je veľká vzdialenosť od Zeme. Rádiové vlny potrebujú nezanedbateľný čas na cestu k družici a späť, napriek tomu, že sa šíria rýchlosťou svetla. Toto časové oneskorenie negatívne vplývalo na kvalitu diaľkových telefónnych hovorov.
Po druhé, ako už bolo povedané, geostacionárna dráha je len v smere rotácie Zeme – nad rovníkom. Obyvatelia žijúci vo väčšej vzdialenosti od rovníka majú väčšie problémy s príjmom. Družice vyžadujú priamu viditeľnosť na prijímač, ak je však družica nízko nad horizontom môže byť tienená budovami, alebo reliefom terénu. Okrem toho, geostacionárna dráha je už dnes tak preplnená a frekvencie takmer obsadená tak, že vzniká riziko vzájomného rádiového rušenia. Výška družice nad obzorom a zemepisná šírka predstavujú spolu tretí problém – slabý signál na mieste príjmu. Geostacionárna družica ožaruje svojím signálom širokú plochu Zeme, ale so vzdialenosťou od rovníka intenzita prijímaného signálu rapídne klesá. S narastajúcou vzdialenosťou od rovníka na sever či juh sa vyžadujú stále väčšie rozmery prijímacej paraboly. Aby sa nedostatky geostacionárnych družíc odstránili, používajú sa na komunikáciu stovky ďalších vzájomne prepojených družíc, ktoré sú menšie a pohybujú sa na nižších dráhach, vo výškach niekoľko stoviek kilometrov nad povrchom Zeme. Ich dráhy prebiehajú pod určitým uhlom k rovníku tak, že signálom pokrývajú prakticky celú zemeguľu. Dnešné moderné satelity sú vybavené niekoľkými prijímacími a vysielacími anténami (pozri obr. 2), ktorých kombinácie umožňujú jednému satelitu vytvoriť lúče pokrývajúce veľké oblasti pre televízne vysielanie a lúče pokrývajúce malé oblasti, ktoré slúžia napr. pre telefónne spojenie. Prepínaním medzi týmito lúčmi podľa potreby je družica schopná spojiť mobilných aj pevných užívateľov na zemskom povrchu. Želám Vám pekný, ničím zlým nerušený deň, s príjemnými zážitkami! Autor 
|