Elektromagnetické javy a ich miesto v elektronike

 6. Meranie výšky mrakodrapu barometrom!

     Milí priatelia! Keďže na stránku sa už pozrelo viac ako 1000 záujemcov, chcel by som sa Vám pri tejto príležitosti znovu poďakovať a dnes naše úvahy trochu odľahčiť. Na Internete voľne koluje príhoda, alebo len anekdota, neviem či je pravdivá, ale je zaujímavá:

7. Čo s magnetickými vektormi M a J a ako „lieči“ magnetizmus?

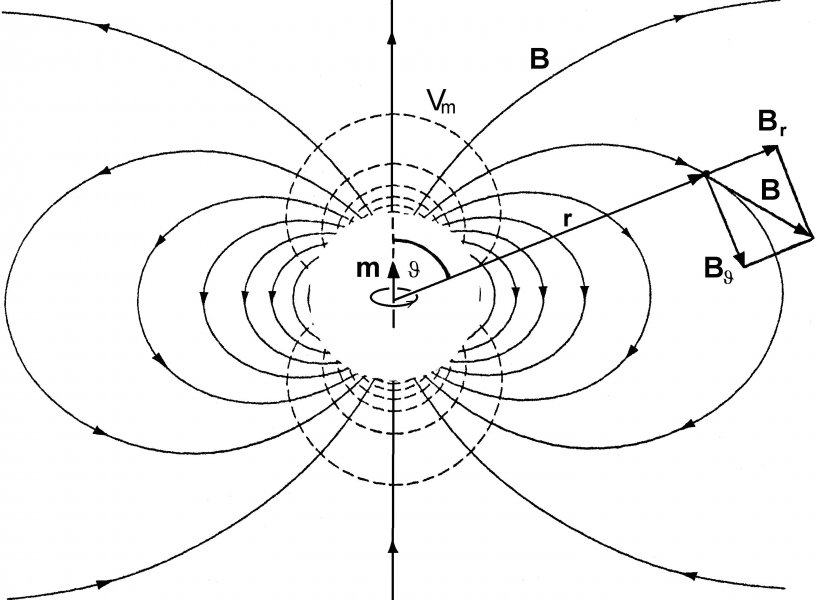
        V látkovom prostredí sme z praktických dôvodov nútení rozdeliť náboje na tie, ktoré patria k „stavebným kameňom“ prostredia, k iónom, atómom, prípadne k molekulám a na viac-menej voľné náboje, ktoré môžu zotrvávať na telesách, rozložené s nejakou objemovou, prípadne plošnou hustotou, ale pod účinkom zdrojov elektromotorických napätí môžu vo vodivom látkovom prostredí vytvárať elektrické prúdy. Taká je napr. situácia v kovoch, kde voľné náboje v kryštalickej mriežke kovu sa môžu, pod účinkom elektrického poľa, pohybovať vybraným smerom a tak vytvárať elektrické prúdy. Elektromagnetické polia v látkovom prostredí sú teda vzbudené niekoľkými zdrojmi – viazanými a voľnými nábojmi a prúdmi elektrických nábojov. Je zrejmé, že voľné náboje, ktoré by vo voľnom priestore vytvorili istú konfiguráciu elektromagnetického poľa, vzbudia v látkovom prostredí celkom inú konfiguráciu, na ktorej sa podieľajú aj viazané náboje. Pôsobením voľných nábojov dochádza v látkach k zložitým procesom elektrickej polarizácie a magnetizácie, pričom v látke vznikajú elektrické dipóly a orientované elementárne prúdové slučky (tieto slučky možno modelovať napr. pohybom elektrónov po klasických dráhach v atóme).

    Elektrický dipól a prúdovú slučku charakterizujeme ich momentami. Elektrický dipól (dvojicu nábojov ±q vo vzájomnej vektorovej vzdialenosti d orientovanej od záporného ku kladnému náboju) charakterizujeme elektrickým dipólovým momentom

p = qd.                                         [C.m =A.s.m]

      Na obr.1 je siločiarami znázornené elektrické pole dipólu; v strede, v bezprostrednej vzdialenosti od dipólu, pole nie je zobrazené, pretože tam nie je dipólovým poľom, ale poľom dvojice rovnako veľkých opačných nábojov. Siločiary začínajú a končia na nábojoch. Ak by sa na siločiare objavil dodatočný náboj, bude sa pohybovať po nej, k tomu z nábojov dipólu, ktorý má opačné znamienko. 

                     

                                          Obr. 1                                                                                 Obr. 2 

Pri definícii magnetického momentu prúdovej slučky vzniká prvá ťažkosť. Tí, ktorí zastávajú názor, že magnetický moment prúdovej slučky má byť vyjadrený iba jej prúdom I a geometriou (a tých je dnes našťastie väčšina), definujú magnetický moment elementárnej slučky výrazom 

m = IS,                                         [A.m²] 

S je vektor plochy S smerujúci na tú stranu plochy, z ktorej prúd kladných nábojov v prúdovej slučke vidieť tiecť proti smeru pohybu hodinových ručičiek. Magnetické pole elementárnej prúdovej slučky je znázornené na obr. 2. Vidíme, že vo veľkej vzdialenosti od slučky je magnetické pole slučky úplne zhodné s poľom dipólu. Tým pádom aj matematické výrazy, ktoré tieto čiary opisujú, musia byť formálne rovnaké (pozri napr. výrazy (2.116) a (6.58) v knihe „Elektromagnetizmus“ na tejto webovej stránke). Lenže pozor! Čo je to za zhoda? Veď je to iba geometrická zhoda nakreslených čiar E a B. V bezprostrednej blízkosti dipólu a slučky sa aj tieto formálne rovnaké čiary diametrálne líšia – elektrické končia na nábojoch a magnetické prechádzajú vnútrajškom slučky a takto sa na seba uzatvárajú (na obrázkoch nie sú zobrazené). Pozríme sa, ako sa bude pohybovať náboj, ktorý sa ocitne najprv v poli elektrického dipólu, a potom v poli elementárnej prúdovej slučky:

      V elektrickom poli dipólu sa náboj bude pohybovať po elektrickej siločiare dipólu, smerom k náboju dipólu opačného znamienka, až skonči na náboji  – dipól tak prestane existovať.

      Ak by sa v magnetickom poli slučky ocitol náboj, ktorý sa voči slučke pohybuje, bude sa špirálovite "ovíjať" okolo niektorej z indukčných čiar B a pozdĺž nej postupovať do miesta známeho ako „magnetické zrkadlo“ (pozri „Elektromagnetizmus“, kapitola 10, obr. 10.5 a 10.6), tu sa odrazí a postupuje k symetricky ležiacemu zrkadlu na uvažovanej indukčnej čiare. Rovinou symetrie je rovina prúdovej slučky. Tak sa pohybujú aj nabité kozmické častice vo Van Allenových radiačných pásoch okolo zemegule, ktoré spôsobujú problémy umelým družiciam Zeme (pozri „Elektromagnetizmus“, kapitola 10). Kde je tu teda podobnosť elektrického a magnetického poľa dipólu a prúdovej slučky? 

      Poznámka: Magnetické momenty spájané s klasickým pohybom elektrónov v atóme sa nazývajú orbitálne magnetické momenty (pozri "Elektromagnetizmus", kapitola 8, odsek 8.1). Elementárne častice majú aj vlastné magnetické momenty a sú kvantované, ale to je kapitola sama o sebe. Vlastný magnetický moment má napríklad aj elektrón, hoci podľa súčasných predstáv teoretickej fyziky je elektrón bodová častica.  

        Venujme sa ale prúdovej slučke z iného pohľadu. Sú ľudia, ktorí si myslia, že uvažovanú prúdovú slučku treba modelovať objektom, ktorý sa musí nutne podobať na elektrický dipól, teda „magnetickým dipólom“ a jeho moment definujú výrazom

j = µ₀m = µ₀IS.                           [Wb.m]

kde µ₀ = 4pi.10^-7 H/m je magnetická konštanta, alebo starší názov permeabilita voľného priestoru (vákua), pi = 3,14159..... je Ludolfovo číslo. Takýto moment opisuje dvojpólový objekt, na ktorého koncoch (podľa rozmeru veličiny) sídlia akési množstvá (magnetické) čohosi, udávané v jednotkách Wb, teda v jednotkách indukčného toku (porovnaj s dipólovým elektrickým momentom p = qd)! Je jasné, že takýto prístup zavádza do teórie elektromagnetizmu dávno zavrhnuté „magnetické množstvá“, alebo "magnetické náboje", ktoré vlastne zavrhol už Ampère. Uvedený moment j sa nazýva magnetický dipólový moment (nazýva sa tiež Coulombov dipólový magnetický moment). Musím povedať, že pod magnetickým momentom m = IS si viem niečo konkrétne fyzikálne predstaviť, ale pod magnetickým  dipólovým momentom  j = µ₀IS nič! Je kuriózne, že československá norma ČSN 01 1305 z 23. 12. 1969 tento časom prekonaný „magnetický dipólový moment“ už neuvádzala, zatiaľ čo novšia verzia z roku 1984 ho znovu zaviedla, ale paralelne s momentom m (nazývaným tiež Ampérov magnetický moment). V poslednej, už slovenskej norme STN ISO 31-5 zo septembra 1997 sa magnetický dipólový moment j uvádza iba v poznámke, ako veličina ICE (položka 5-27, pozn.). Z uvedeného vidieť, že aj tvorcovia noriem majú v týchto otázkach problémy. Pripomínam, že SI-sústava bola zavedená 11. generálnou konferenciou pre miery a váhy (CGPM) v roku 1960 a v Československu bola uzákonená Uznesením vlády č. 7/1974 v roku 1974 (SI-sústava jednotiek je založená na metrickej sústave, ktorá sa na našom území začala používať hneď po jej vzniku, v roku 1871, medzitým sa v technickej praxi  začala používať MKSA-sústava).

    Elektrickú polarizáciu látok udáva vektor elektrickej polarizácie P, ako objemovú hustotu elektrických dipólových momentov, teda  

P = np,                                         [C.m^-2 = A.s.m^-2] 

kde n je koncentrácia dipólových momentov v látke. Tu nevznikajú žiadne problémy (pozri na tejto webovej stránke učebnicu "Elektromagnetizmus", kapitola 4, odsek 4.1).

        Pri opise magnetizácie látok sa znovu dostávame do ťažkostí, pretože dva zavedené magnetické momenty  m  a j poskytujú možnosť vyjadriť magnetizačný stav látky pomocou dvoch veličín: 

a)  Prvou veličinou je vektor magnetizácie M, ako objemová hustota magnetických momentov m v látke. Podľa tejto definície

M = nm,                                 [A. m^-1] 

kde n je koncentrácia magnetických momentov (elementárnych prúdových slučiek). Podľa rozmeru, veličina M  svojou veľkosťou predstavuje hustotu viazaného mikroskopického plošného prúdu, ktorý by obtekal plášť vybraného elementárneho valčeka z magnetizovaného materiálu a vektor M by mal smere osi valčeka. Takto definovaná veličina sa dá ľahko pochopiť (pozri "Elektromagnetizmus", kapitola 8. 2. 1). 

b)  Druhou veličinou je vektor magnetickej polarizácie J, ako objemová hustota magnetických „dipólových“ momentov j. Podľa tejto definície 

J = nj = µ₀nm =  µ₀M.                                 [T] 

    Vektorová veličina J má rozmer a jednotku magnetickej indukcie – tesla [T] a niektorí autori nie veľmi presvedčivo tvrdia, že „predstavuje príspevok k magnetickej indukcii spôsobený látkou“ – veď vektor magnetizácie M predstavuje presne to isté a pritom nie je rozporuplný. Podľa rozmeru vidíme, že to nie je pravý magnetizačný vektor, ale skutočne akýsi „polarizačný“ vektor. Lenže pojmy ako pól, dipól a polarizácia v modernej teórii magnetizmu nemajú čo hľadať! Možno ich tolerovať v geografii, kde pojem zemský magnetický pól má presne vymedzený význam (miesto na zemeguli, kde vektor magnetickej indukcie B zemského magnetického poľa na povrchu Zeme je maximálna, na južnom póle smeruje kolmo nahor a na severnom póle kolmo nadol). S nevôľou musíme prijať aj pojem póly tyčového magnetu a póly na rotoroch, resp. statoroch v rôznych elektrických strojoch, ale s veľkou opatrnosťou, pretože napríklad na tyčovom magnete ich nemožno presne lokalizovať a po rozlomení magnetu vzniknú na fragmentoch dva nové „póly“. Musíme ich prijať iba preto, že v magnetickej terminológii jednoducho nemáme na to označenie vhodnejší názov.  

      Pôvod vektora J (a tým aj vektora j) tkvie v starej CGS-sústave, kde základným vektorom magnetizmu bol vektor H, ako produkt magnetických nábojov. Tak je zavedená aj intenzita elektrického poľa E v elektrine. V súčasných učebniciach písaných v SI-sústave vektory J a  j pramenia zo snahy hľadať analógie tam, kde ich niet – medzi elektrickým a magnetickým poľom. Každé z polí má úplne iné silové účinky, a to treba mať vždy na pamäti. Opravnene sa možno spýtať, prečo v elektrine stačí jeden polarizačný vektor P a v magnetizme treba naraz dva – jeden magnetizačný M a druhý polarizačný J ?

        Vektor magnetickej polarizácie J sa objavil v českej a slovenskej odbornej literatúre (používajúcej MKSA-sústavu a neskôr SI-sústavu) po druhej svetovej vojne. V ruskej, ani v západnej literatúre (s výnimkou bývalej NDR) v knihách písaných v SI-sústave, alebo v staršej MKSA-sústave sa mi ho nepodarilo objaviť (hoci sa zďaleka nemôžem zaručiť, že sa niekde nenachádza). Napodiv, v slovenskej norme STN ISO 31-5 zo septembra 1997 inkriminovaná magnetická polarizácia J = B – µ₀H  [T] (pozri položku 5-29) sa uvádza, ako vektor rovnocenný so skutočným  vektorom magnetizácie M = B/µ₀ – H  [A.m^-1]!

        Záver: Vektory magnetickej polarizácie J = µ₀nm = nj =  µ₀M = B – µ₀H [T] a magnetický dipólový moment j  = µ₀m treba bez ohľadu na autority zavrhnúť, pretože iba zbytočne zaťažujú modernú elektromagnetickú teóriu, zneisťujú študenta a sú doslova škodlivé. Magnetizačnými vektormi sú jednoznačne iba vektory M = nm = B/µ₀ – H  [A.m^-1] a m = IS  [A.m²] !

*****

        Nakoniec sa mi žiada povedať niekoľko slov o „liečivých“ účinkoch magnetizmu, hoci táto problematika do danej úvahy ani veľmi nepatrí. Mnohí liečitelia (aj s lekárskymi titulmi) ponúkajú, za ťažké peniaze, magnety a rôzne pomôcky vyrobené z magnetov na liečbu všetkého. Magnetizmus – a hlavne feromagnetizmus – je stále trochu tajomný jav, preto sa dá dobre zneužívať a na tom sa dá výdatne ryžovať. Nenadarmo sa v diele "Encyclopedia Britannica" doslova píše: "Few subjects in science are more difficult to understand than magnetism". Seriózne však možno povedať iba to, že telové kvapaliny sú elektrolyty a tie sú v živom organizme v pohybe. Ak sa dostanú pod účinok statického magnetického poľa, toto pole bezo sporu bude vplývať na charakter pohybu iónov v elektrolyte. Je však otázkou, či bude zvyšovať prietočnosť ciev, alebo zvyšovať ukladanie nejakých telových produktov, napríklad lipidov, v cievach. Ak magnetické pole je časovo premenné, v takomto prípade pole s cievami "cvičí", a jeho účinok môže byť naozaj pozitívny !?. Neviem, či existujú spoľahlivé štúdie o týchto pôsobeniach, pretože keď mi v kúpeľoch nasadzovali prúdové cievky pri magnetoterapii a ja som sa pýtal na pôsobenie a účinky, nikto z odborného personálu mi nevedel k tomu nič presvedčivého povedať. (Moderný lekár by mal mať okrem medicínskeho, aj veľmi dobré fyzikálne vzdelanie, ináč môže skĺznuť do pozície iba obyčajného felčiara!). Magnetizmus môže mať aj pozitívne psychologické účinky (akýsi placebo efekt), ak bude dokázané, že nemá tie negatívne. Rozhodne ale škodí platobným kartám, a to dvoma spôsobmi – poškodzuje magnetický záznam na karte a znižuje stav konta nezmyselným výdavkami za magnetické pomôcky! Želám Vám príjemný deň a nenechajte sa podvádzať ! Autor

4. 7. 2008
 

8. Requiem nad spinovým echom.

        Moderné diagnostické zariadenie JMR- (NMR)-tomograf, ktorému som venoval úvahu 5, používa na snímanie špeciálne metodiky a to metodiku voľnej precesie, alebo voľnej indukcie (FID – free induction decay), prípadne metodiku spinového echa, ktoré spočívajú v tom, že sa vyšetrované tkanivá ožarujú nie spojitým elektromagnetickým vysokofrekvenčným (vf) žiarením, ale vf žiarením vo tvare elektromagnetických vf impulzov, v ktorých sú polia na rezonančnej JMR frekvencii vhodne polarizované a signály, ktoré sa pozorujú, sú odozvami látky po vf impulze. Táto metodika JMR bola známa dávno pred začiatkom konštrukcie tomografov. Metodika spinového echa (niekedy nazývaná "impulzná JMR") sa vo svojich začiatkoch využívala na meranie relaxačných časov v látkach, ktoré obsahujú protóny (jadrá vodíka). Relaxačné časy určujú dynamiku energetickej výmeny protónov s ich okolím, ktoré sa nazýva mriežkou (spin-mriežková relaxácia, relaxačný čas T₁), ako aj energetickú výmenu medzi samotnými protónmi, alebo spinmi (spin-spinová relaxácia, relaxačný čas T₂). Merania  relaxačných časov vtedy umožňovali napr. výber vhodných kvapalných kryštálov na výrobu kvapalnokryštalických displejov (LCD - liquid crystal display). Takéto merania spinových ech sme na mojom bývalom pracovisku, na Prírodovedeckej fakulte Univerzity Komenského v Bratislave, vykonávali už v šesťdesiatych rokoch uplynulého storočia. V tomto zmysle sa Univerzita Komenského už v šesťdesiatých rokoch podieľala na vývoji NMR-tomografu. Na tomto mieste treba povedať niekoľko slov o histórii skúmania javu spinového echa na Univerzite Komenského:      

      V školskom roku 1959-60 som končil  diplomovú prácu na tému „Meranie magnetických polí metódami jadrovej magnetickej rezonancie“ na PriF UK a spolu so mnou dvaja moji kolegovia pracovali na veľmi zaujímavých diplomových témach. Jeden pracoval na konštrukcii generátora impulznej zmesi, a druhý konštruoval vf generátor a prijímač signálu spinového echa (dnes sa prístroje kupujú, my sme si ich museli postaviť). V tom čase jediný, nám v dosahu známy spin-echo spektrometer – predchodca dnešných NMR-tomografov, existoval na Physikalisches Institut der K-M Universität v Lipsku, u Profesora Lösche-ho, v pracovnej skupine nedávno zosnulého Profesora Pfeifera, ďalší bol vo Francúzsku. Na východe sa problematikou NMR zaoberali v Košiciach, v Krakove, vo vtedajšom Sovietskom zväze v Leningrade, v Moskve a v Kazani (tam ale robili hlavne EPR). Iné pracoviská mi nie sú známe, ale  na žiadnom z uvedených sa nerobila metodika spinového echa.

        Spomínaní dvaja kolegovia dokončovali svoj spin-echo spektrometer v posledných dňoch roku 1959 a s vedúcim diplomovej práce uzavreli stávku, že získajú signál spinového echa do Nového roku 1960. Vedúci sľúbil, že ak sa im to podarí, dogúľa po Stalinovom námestí (dnešné Námestie SNP) z Tety na začiatku Dunajskej ulice,  na katedru sud piva (vtedajšia Katedra experimentálnej fyziky PriF UK sídlila pri Trojičnom kostole na Šmeralovej ulici, dnes je to lokalita na konci Župného námestia, na mieste, kde sa nachádza budova Ministerstva spravodlivosti). Písal sa 31. december 1959.  My, ostatní diplomanti zhromaždení na katedre, sme určite čakali  viac na signál, ako na to pivo. Milošovi a Silvovi (tak sa priatelia volali) sa poobede na Silvestra, skutočne podarilo signál zo šumu vydolovať. Bol to jeden z mojich najkrajších Silvestrov – Bratislava mala spinové echo – impulznú jadrovú magnetickú rezonanciu! To v tom čase nemali ani v blízkej Viedni, ani v Prahe! Dnes by o tom informovali masmédia, vtedy to  pre ne nebolo nič mimoriadne, a my sme pracovali pre radosť z práce a nie pre reklamu.

          Dvojimpulzovú metódu spinového echa prvýkrát  publikoval  E. L. Hahn (Hahn E. L., Phys. Rev. 80 (1950), 580), druhú, mnohoimpulzovú metódu publikovali H. Y. Carr a nositeľ Nobelovej ceny za fyziku E. M. Purcell (Carr  H. Y., Purcell E. M., Phys. Rev. 94 (1954), 630), fyzici na Harvardovej univerzite. Volala sa Carr-Purcellova metóda, dnes ju – z akýchsi dôvodov – volajú "fast spin echo". Nám sa tieto experimenty podarilo realizovať a dotvoriť iba o 9, resp. 5 rokov neskôr a určite s neporovnateľne nižšími nákladmi ako kolegom v Amerike a bez možnosti isť sa pozrieť, ako to tí Američania robia.

        Prvá publikácia o našom spin-echo spektrometri vyšla v roku 1963 (Lampert M., Šranko S., Šurka Š., Tirpák A., Matematicko-fyzikálny časopis SAV, 13, 1-1963). Žiaľ, moji traja kolegovia a priatelia už nie sú medzi nami a spinové echo na našej fakulte je už tiež minulosťou - ...ET LUX PERPETUA LUCEAT EIS. 

        Prví dvaja kolegovia po úspešnej obhajobe diplomových prác, po štátnici a promócii z fakulty odišli a mňa problematika tak zaujala, že som sa jej venoval niekoľko ďalších rokov. Postavili sme nový spin-echo spektrometer, na ktorom sme robili zaujímavé publikované výskumy o magnetickej relaxácii v kvapalinách, dokonca publikované aj v spolupráci s Physikalisches Institut der K-M Universität v Lipsku. V roku 1963 bola oponovaná a obhájená výskumná správa na tému „Spin-echo spektrometer“ a v roku 1966 bol publikovaný  článok ku konštrukcii spektrometra (Šurka Š., Tirpák A., Acta F. R. N. Univ. Comen. X.-7.-Physica VII., 1966). Všetky nasledujúce obrázky a oscilogramy sú originály z uvedených našich publikácií.

        Týmto historickým exkurzom chcem predovšetkým povedať, že to, o čom sa dnes píše vo Wikipédii a o čom možno čítať na serveri Google ako o novinke, sme my robili na profesionálnej úrovni už takmer pred 50 rokmi. Čo ma však skľučuje je skutočnosť, že v príspevkoch na internete, pri dnešných prístrojových možnostiach, som nenašiel jediný skutočný osciloskopický záznam spinového echa a voľnej indukcie (FID), iba gýčovito farebné animácie,  ktorými sa autori ťažkopádne pokúšajú vysvetliť, čo je spinové echo a ako vzniká. Myslím, že autentický, osciloskopický, záznam nenahradí žiadna animácia a  preto v ďalšom prezentujem niekoľko našich osciloskopických záznamov spinového echa. Nuž, veľa vecí sa dnes robí povrchne a iba na vonkajší efekt. Keby som nevedel o čo ide, tak to vôbec nepochopím.

*****

        Tým, ktorí sa rozhodli čítať túto úvahu ďalej, odporúčam si prečítať najprv  úvahu 5. Kto sa chce o problematike dozvedieť o niečo viac, odporúčam mu  v  učebnici "Elektromagnetizmus",  v kapitole 8, si prečítať odsek  8. 5. 4 "Jadrová magnetická rezonancia  a elektrónová paramagnetická rezonancia".

                                                         

                                                                                          Obr. 1

      Aj impulzná jadrová magnetická rezonancia, teda spinové echo, je selektívna absorpcia vf elektromagnetickej energie systémom protónov vo vode uložených v silnom magnetickom poli B₀, a platí rovnaká rezonančná podmienka ako tá, ktorá je uvedená v úvahe 5 v súvislosti s JMR-tomografom. Rezonančná podmienka v numerickom tvare, po dosadení konštánt znie f₀ = 42,577 365 92× B₀ MHz (B₀ v jednotkách T) a pre vodu nezávisí od ničoho iného, iba od magnetickej indukcie B₀. Je dobré na tomto mieste pripomenúť, že rezonančná frekvencia f₀ je zhodná s frekvenciou Larmorovej precesie magnetických momentov protónov v magnetickom poli B₀.

      Na rozdiel od spojitej jadrovej magnetickej rezonancie, pri metóde spinového echa sa vzorka vody v ampulke, umiestnenej v silnom magnetickom poli B₀, ožaruje silnými vf elektromagnetickými impulzmi na rezonančnej frekvencii f₀. Rôzne pohľady na spin-echo spektrometer sú na obr. 2, 3 a 4. Na obr. 2 je celkový pohľad na aparatúru, na obr. 3 je pohľad na elektronickú časť, a na obr. 4 je pohľad do štrbiny magnetu. 

               

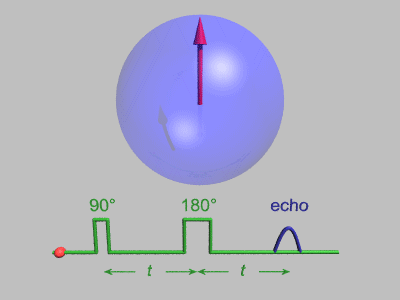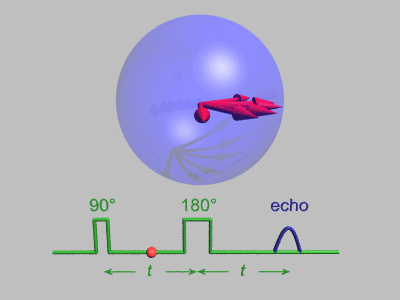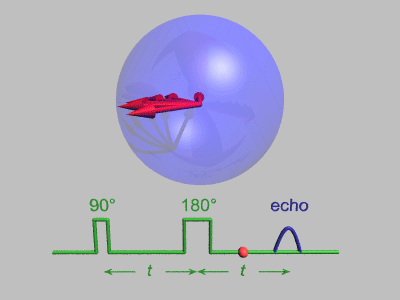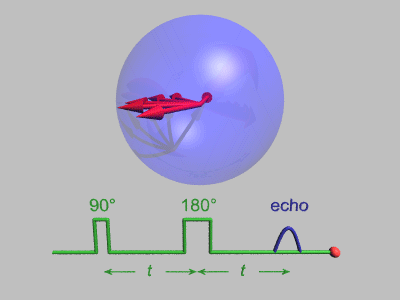
                                                                                      Obr. 4a

      Keď sa do cievky vloží ampulka so skúmanou látkou, po krátkom čase - v závislosti od dĺžky spin-mriežkového relaxačného času T₁ - silné statické magnetické pole B₀ magnetu S-J indukuje vektor statickej protónovej magnetizácie M₀ (pojem známy z úvahy 7 - zo všetkých možných magnetizácií v látke nás bude teraz zaujímať iba protónová magnetizácia, pretože iba ona reaguje na vf pole s rezonančnou frekvenciou). Vektor M₀ je výslednicou protónových magnetických momentov, ktoré precesujú  na ploche kužeľa, ktorého os  splýva  so smerom B₀.

      Cievka v štrbine magnetu plní dve funkcie: z vysielača (násobič frekvencie 20 MHz) privádza vf impulz na vzorku látky v ampulke a po skončení vf impulzu slúži ako prijímacia cievka na vstupe selektívneho prijímača (20 MHz) signálov voľnej indukcie (FID), prípadne spinového echa. 

      Pri Hahnovej metóde, v každom cykle pôsobia na vzorku dva  vf impulzy: prvý, 90⁰-vý, impulz otočí vektor magnetizácie M₀ (a teda celý kužeľ) do priečnej roviny, kolmej na smer S-J silného magnetického poľa (pozri obr. 1). Vektor magnetizácie sa po preklopení pohybuje veľmi zložito - kužeľ protónových momentov precesuje okolo smeru B₀. V cievke sa chová ako maličký  magnetík rotujúci v rovine štrbiny, okolo smeru S-J ("magnetík" ako keby postupne "strácal silu"). Na koncoch cievky indukuje vf napätie s exponenciálne klesajúcou amplitúdou, ktoré prijímač zosilní, spracuje a privedie na synchroskop (synchronizovaný osciloskop). Situáciu na vstupe prijímača vidieť v animácii na obr. 5, a na osciloskope  na obr. 6 za prvým,  90⁰-vým, impulzom ("ihlový" impulz na obrázku nevidieť). Je to zanikajúce napätie voľnej indukcie (alebo navoľnej precesie) FID.

    Zánik vektora magnetizácie v priečnej rovine spôsobuje skutočnosť, že magnetické polia v miestach jednotlivých protónov sú rôzne a to v dôsledku prirodzenej nehomogenity poľa magnetu, ako aj vzájomnej spin-spinovej interakcie. Táto interakcia sa prejavuje tak, že jeden spin v mieste druhého vytvára svoje magnetické pole a tým sa rezonančná podmienka rozmazáva. Na základe týchto faktov sa bude preklopený vektor magnetizácie v  priečnej rovine rozpadávať do stále rovnomernejšie rozvinutej ružice (tá, samozrejme, v priečnej rovine rotuje so strednou frekvenciou f₀), význačný smer v priečnej rovine sa stráca, v dôsledku čoho signál v cievke nakoniec úplne zanikne. Taká je situácia pred druhým impulzom.  

      Rozpadnutá ružica síce nakoniec v cievke žiadne napätie neindukuje, ale zachováva si svoju spinovú pamäť. Ak sa po dostatočne dlhom čase privedie na cievku druhý, 180⁰-vý, impulz (pozri obr.5, 6), ružica sa otočí o 180^o stupňov, jednotlivé zložky vektora magnetizácie sa začnú zbiehať a po rovnakom čase, aký uplynul medzi prvým a druhým impulzom sa vytvorí v priečnej rovine znovu výrazná magnetizácia, ktorá bude v cievke znovu indukovať vf napätie. Tento signál sa volá spinové echo (ozvena), ktoré dobre vidieť na obr.5, 6. Niekedy sa vznik spinového echa vysvetľuje trochu podivným športovým zápolením, že skupina rôzne výkonných športovcov-bežcov sa postaví na štartovaciu čiaru na bežeckej dráhe, kde ich štartér výstrelom (prvý impulz) odštartuje. Športovci bežia rôznou rýchlosťou a za istý čas prejdú rôzne dráhy tak, že skupina sa rozpadne na jednotlivých bežcov. Druhým výstrelom (druhý impulz) ich štartér otočí a nechá bežať každého svojou pôvodnou rýchlosťou, ale naspäť. Po rovnakom čase ako medzi výstrelmi sa všetci v skupine vrátia naraz na štartovaciu čiaru (to je obraz spinového echa!).

        Ak sa vzdialenosť medzi prvým a druhým impulzom bude zväčšovať, bude sa vzďaľovať aj echo, pričom jeho amplitúda bude exponenciálne klesať. Amplitúda echa klesá v dôsledku nereverzibilnej spin-spinovej interakcie (spinová pamäť sa stráca). Charakteristický čas exponenciálneho poklesu amplitúdy sa v prvom priblížení rovná  relaxačnému času T₂ spin-spinovej interakcie. Netreba zabudnúť, že celý systém spinov má tendenciu sa znovu otočiť do smeru B₀, kam relaxuje s charakteristickým časom T₁ (spin-mriežkový relaxačný čas) a tam vytvoriť pôvodnú  magnetizáciu M₀.
 

        

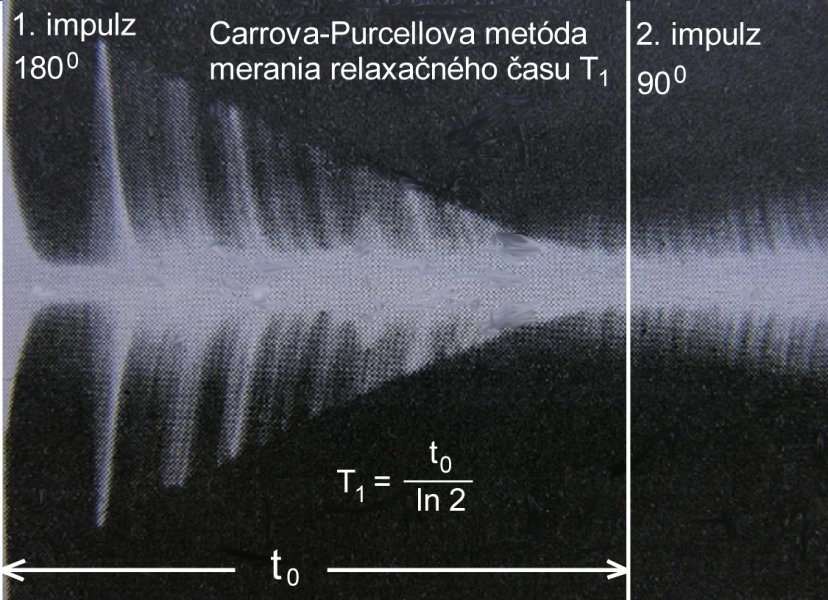
                                                      Obr.7                                                                                               Obr.8  

           Elegantnejšia a na meranie spin-spinového relaxačnému času T₂ presnejšia je Carrova-Purcellova metóda, pri ktorej sa na vzorku látky po druhom, Hahnovom, impulze naloží celá séria 180⁰-vých impulzov v dvojnásobnej vzdialenosti prvého a druhého impulzu. Ak totiž po rozpade echa do ružice ju znovu otočíme o 180⁰-ov, sformuje sa ďalšie echo s menšou amplitúdou, atď. Vznikne séria ech, ktorú vidieť na obr. 7. Z exponenciálnej obálky ech možno určiť relaxačný čas T₂. Na obr. 8 je zobrazená Carrova-Purcellova séria ech v obyčajne vode. Vzhľadom na relatívne dlhý relaxačný čas T₂ ≈ 1,5 s (v destilovanej, odplynenej vode je tento čas T₂ ≈ 3,6 s) musí sa použiť dlhá Carrova-Purcellova séria s veľkým množstvom 180⁰-vých impulzov a ech, takže jednotlivé echá na obrazovke osciloskopu splývajú.                        

                 

                                            Obr. 9                                                                                           Obr.10

        Na obr. 9 je znázornená Hahnova trojimpulzová séria typických piatich ech používaná na meranie relaxačného času T₁, ale na to je výhodnejšia a jednoduchšia Carrova-Purcellova dvojimpulzová metóda, ktorá je demonštrovaná oscilogramom na obr. 10. Prvý, 180⁰-vý impulz, otočí vektor magnetizácie do protismeru magnetického poľa B₀, odtiaľ sa tento vracia do pôvodného smeru poľa B₀ exponenciálne s charakteristickým časom T₁, pričom prechádza cez nulovú hodnotu. Za prvým impulzom nie je žiadna voľná indukcia. Druhý impulz, 90⁰-vý, je sondovací, ak leží bezprostredne za prvým impulzom, je za ním intenzívna voľná indukcia (FID). S jeho vzďaľovaním voľná indukcia klesá, až pri vzdialenosti t₀ od prvého impulzu je nulová a pri ďalšom vzďaľovaní  sa bude znovu zväčšovať. T₁ sa vypočíta z jednoduchého vzťahu: T₁ = t₀/ln2. Treba povedať, že čím dlhšie sú relaxačné časy, tým obťažnejšie boli ich merania, pretože pred každou novou sériou bolo treba čakať na ustálenie termickej rovnováhy v systéme protónových spinov s mriežkou, pritom táto doba je cca 5T₁. Napríklad u benzénu, ktorého T₁ = 19,3 s (v acetóne 15,0 s) bolo treba čakať na ustálenie takmer 100 sekúnd, resp. 75 sekúnd a až potom sa mohla poslať nová séria impulzov.

      Veľkým handicapom našich meraní bola neexistencia výpočtovej techniky, ktorá sa vtedy obmedzovala na logaritmické pravítko (hliníkové sa vozili z NDR - u nás boli iba drevené a plastové) a ručné, kľukové kalkulačky. Takmer všetky osciloskopické priebehy sa museli z obrazovky osciloskopu fotografovať, filmy sa museli mokrou cestou vyvolávať a výsledky pod zväčšovákom graficky spracovať, čím vyhodnocovania zaberali veľa času a metódam to na presnosti tiež nepridávalo. S dnešnými možnosťami sa to nedá porovnať. Vážení priatelia, ak ste vydržali do konca, ďakujem a želám Vám pekný deň! Autor

17. 7. 2008

9. Nedotýkajte sa (nielen) spadnutých drôtov!  

        Oheň je dobrý sluha, ale zlý pán. Toto otrepané príslovie ale oveľa viac ako pre oheň, platí pre elektrinu. V domácnosti neodborné používanie elektrických zariadení, alebo neodborná inštalácia spôsobuje nielen materiálne škody, ale ohrozujú aj ľudské životy. Oveľa väčšie bývajú následky, ak sa havária stane na prenosovej trase vysokých elektrických výkonov. Aby sme nadobudli predstavu o aké výkony ide, možno uviesť, že napríklad elektráreň Gabčíkovo svojimi  8 turbogenerátormi, z ktorých každý vyrába  90 MW, dodáva do energetickej siete celkovo 720 MW a tie sa prenášajú pri primárnom napätí 400 kV. Budeme analyzovať príklad, čo sa môže stať, ak  na vedení veľmi vysokého napätia vznikne havária. Predpokladajme teda, že:

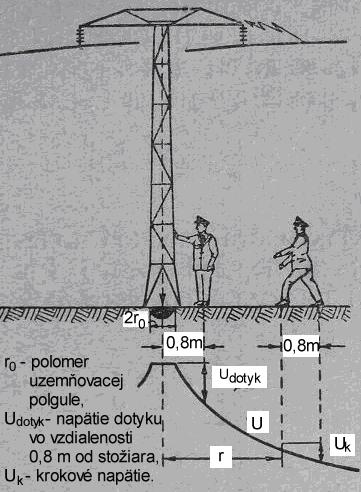
        Elektrický stožiar vysokého napätia U = 400 kV je uzemnený vodivou polguľou polomeru r₀ = 60 cm zakopanou v zemi, ako na obr. 1. Na vedení vznikla porucha tak, že nastal skrat medzi vedením (jednou fázou) a stožiarom. Treba vypočítať, pod akým napätím sa ocitne človek, ktorý urobí krok dĺžky k = 80 cm smerom k stožiaru, alebo od neho, vo vzdialenosti: a) r₁ = 100 m, alebo b) r₂ = 25 m od uzemnenia. Toto napätie U_k sa nazýva krokovým napätím. Konduktivita pôdy je s = 10^-2 S/m. 

                           

                                              Obr. 1                                                                                 Obr. 2 

        Ak by takýto prípad naozaj nastal, bola by to veľká havária na energetickej sústave, k čomu by vedeli povedať svoje energetici. My posúdime takýto prípad z fyzikálneho pohľadu a z pohľadu ohrozenia ľudí. Uzemnenie je schématicky znázornené na obrázku. K riešeniu našej úlohy potrebujeme vypočítať odpor uzemnenia R, efektívnu hodnotu prúdu, ktorý tečie do uzemnenia a jeho objemovú hustotu ako funkciu r, z nej vypočítať efektívnu intenzitu elektrického poľa v pôde a na povrchu zeme (tiež ako funkciu r) a nakoniec efektívne krokové napätie. 

        Celkový odpor uzemnenia vypočítame integráciou (sčítaním) elementárnych priečnych odporov dR polguľových vrstiev hrúbky dr, teda dR = dr/(2pi×sr²) od polomeru r₀ do nekonečna, pi = 3,14159..... je Ludolfovo číslo (pozri obr. 2). Takáto integrácia vedie k hodnote odporu R = 1/(2pi×sr₀) = 26,5 ohmov. Pri výpočte sme sa dopustili istej nepresnosti, pretože sme predpokladali, že zemeguľa zaberá celý polpriestor, čo nie je pravda, ale je dosť objemná, aby sme si toto priblíženie mohli dovoliť.

    Celkový efektívny prúd je obrovský: I = U/R ≈ 15 000 A  (dodávaný činný výkon P = UI ≈ 6 GW!). Ak to energetická sústava prežije, potom objemová hustota prúdu a hustota prúdu na povrchu zeme vo vzdialenosti r bude J = I/(2pir²) = (sr₀U/r²) a efektívna intenzita elektrického poľa vo vzdialenosti r bude E = J/s = r₀U/r². Ako vektor je intenzita kolmá na povrch guľovej plochy uzemnenia, na povrchu terénu sleduje povrch. Tesne nad povrchom je rovnaká ako na povrchu (platia hraničné podmienky – elektrické polia sú k rozhraniu tangenciálne, a na rozhraní  sú rovnaké). Intenzita sa ale bude deformovať, ak sú na povrchu vodivé predmety.

        Krokové napätie sa vypočíta tak, že sa integrujú napäťové prírastky dU_k  = Edr po dĺžke jedného kroku od r po r ± k  [(+) platí pre pohyb od stožiara a (–) pre pohyb k nemu]. Integrácia poskytuje pre krokové napätie výraz:  

U_k  = r₀kU/[r(r ± k)].

Pri pohybe vo vzdialenosti r₁ = 100m od stožiara a k nemu bude krokové napätie približne rovnaké, a to

U_k1 ≈ 19 V.

Pri pohybe vo vzdialenosti r₂ = 25 m od stožiara je krokové napätie

U_k2 ≈ 298 V

a pri pohybe k nemu je krokové napätie 

U_k2 ≈ 317 V!!!

      Ak vezmeme do úvahy, že podľa normy bezpečné striedavé napätie v suchom prostredí je do 25 V a jednosmerné do 60 V, vidíme, že človek, ktorý by vo vzdialenosti 25 m urobil krok k stožiaru, alebo od neho, by bol smrteľne ohrozený. Teoreticky by mohol „bezpečne“ chodiť po sústredných kružniciach okolo stožiara, pretože na týchto kružniciach je potenciál konštantný (kružnice sú ekvipotenciály). Z nebezpečnej zóny by musel „vyskákať“, ale so spojenými nohami (len neviem či už takto niekto niekedy vyskákal!). Striedavé napätie do 19 V sa v norme udáva ako bezpečné, ale neviem, kam to napätie možno na telo pripojiť a v akej telesnej aj psychickej kondícii musí byť človek, aby sa mu naozaj nič nestalo (môže byť napr. spotený, alebo musí byť suchý a pod.?). Vo vlhkom prostredí je  bezpečné striedavé napätie maximálne 6 V a jednosmerné maximálne 15 V. Striedavé napätie 19 V aj keď je „úradne“ bezpečné, v rozkroku by mohlo dosť nepríjemne štekliť. Dotykové napätie U_dotyk v danej situácii je veľmi vysoké a smrteľne nebezpečné! Lepšie by bolo sa do opísanej situácie nedostať. Želám Vám pekný, ničím zlým nerušený deň! Autor   

10. Ako sa analyzujú kapacitné elektrické siete?

          Známy nemecký fyzik Gustav Robert Kirchhoff v roku 1845, ešte ako mladý, 21-ročný študent na Univerzite v Königsbergu (terajší Kaliningrad) sformuloval dva zákony (alebo priliehavejšie pomenovanie by bolo "pravidlá"), ktoré sa dajú výhodne použiť pri analýze elektrických sieti. Pod názvom elektrická sieť rozumieme akékoľvek, samozrejme účelné, pospájanie elektrotechnických prvkov (rezistorov, kondenzátorov, indukčností) a zdrojov elektromotorických napätí (EMN). Prvky siete vytvárajú vetvy a tie sú pospájané uzlami. V sieti tak možno vytvárať myslené uzavreté slučky. Analýza siete spočíva vo výpočte napätí, prúdov, prípadne nábojov na zadaných prvkoch siete a pri zadaných EMN zdrojov.

          Kirchhoffove zákony sú založené na platnosti dvoch zákonov elektromagnetizmu: a) na zákone zachovania elektrického náboja, b) na zákone, ktorý vyjadruje skutočnosť, že integrál intenzity elektrického poľa na uzavretej dráhe sa rovná nule (stacionárny prípad), alebo sa rovná zápornej časovej zmene indukčného magnetického toku (nestacionárny prípad – známa kompletná Maxwellova rovnica o rotácii intenzity elektrického poľa). Pre nestacionárne siete však prvý Kirchhoffov zákon nemusí vždy platiť. Preto tvrdím, že tieto zákony nie sú v skutočnosti zákony,  a bolo by vhodnejšie ich nazývať Kirchhoffove pravidlá pre analýzu elektrických sietí (the Kirchhoff´s rules, die Kirchhoffsche Regeln). Kirchhoff svoje zákony formuloval pre čisto odporové, teda stacionárne siete, pretože v čase jeho mladosti striedavé napätia ešte neexistovali. Tieto zákony sa najčastejšie uvádzajú v tvare:

      Prvý Kirchhoffov zákon (pravidlo uzlov): Algebrický súčet všetkých ustálených prúdov I_i (i = 1,2, …., l) v uzle elektrickej siete sa rovná nule.

      Druhý Kirchhoffov zákon (pravidlo slučiek): Algebrický súčet elektromotorických napätí zdrojov U_0i (i = 1,2, …, n) v uzavretej slučke elektrickej siete sa rovná  algebrickému súčtu potenciálnych spádov R_iI_i (i = 1,2, …., m) na jednotlivých odporoch obvodu.

      Kirchhoffove zákony sa dajú zovšeobecniť aj pre striedavé, impedančné siete, nedajú sa použiť pre čisto kapacitné siete s jednosmernými zdrojmi, pretože v nich prúdy netečú. Tento prípad treba posúdiť osobitne.

Kapacitné elektrické siete s jednosmernými zdrojmi.

      Kapacitné elektrické siete pozostávajú iba z kondenzátorov a z jednosmerných zdrojov EMN, ktorých vnútorný odpor nie je podstatný. Kondenzátory sú účelne pospájané, napr. za sebou (sériovo) a spolu so zdrojom vytvoria uzavretú slučku, alebo sú pospájané vedľa seba uzlami (paralelne), prípadne vytvárajú kombinácie oboch predchádzajúcich spojení. Možno tiež vytvárať spojenia vyššej zložitosti, nazývané mostíkové, ktoré nie sú kombináciou predchádzajúcich. Takto môžu vzniknúť zložité elektrostatické siete, ktoré sú v praxi zriedkavejšie ako odporové siete a možno preto sa im venuje menšia pozornosť. V kapacitnej sieti sú obyčajne  zadané EMN zdrojov a kapacity kondenzátorov, a pri analýze sa hľadajú náboje, alebo napätia na kondenzátoroch. 

      V učebnici „Elektromagnetizmus“, v kapitole 3, odsek 3. 6 som sformuloval dve pravidlá na analýzu kapacitných sietí, ktoré sa formálne podobajú na Kirchhoffove zákony (v učebnici sú uvedené v opačnom poradí ako v tejto úvahe). Nazývam ich pravidlo uzlov a pravidlo slučiek pre kapacitné siete. Treba hneď na začiatku povedať, že pravidlá  sú pôvodné, neviem o tom, aby boli predtým publikované.  Tak ako Kirchhoffové zákony, neprinášajú  ani tieto pravidlá, nové zákony do elektromagnetizmu, novou je ale systematizácia  známych zákonov (zákon zachovania náboja a dráhový integrál intenzity elektrického poľa) a ich aplikácia na kapacitnú sieť. Nakoniec, ani mladý Kirchhoff neurobil viac, keď formuloval svoje zákony pre odporové siete.

Prvé pravidlo (pravidlo uzlov):          

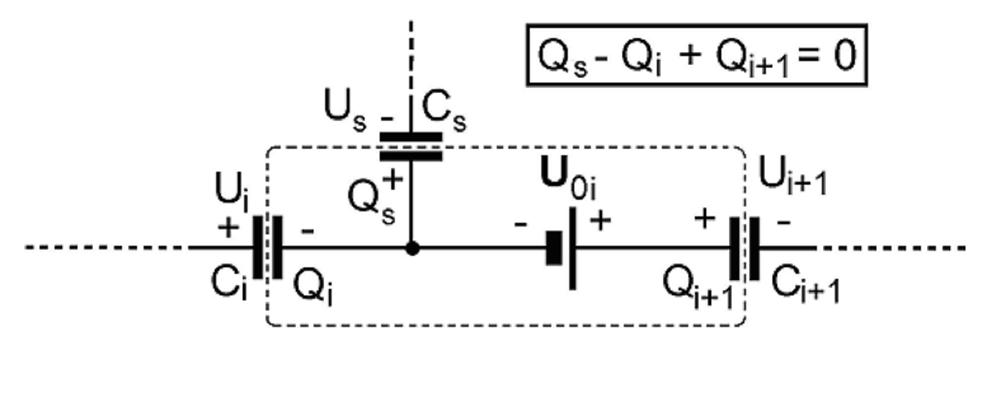
    Pri formulácii pravidiel pre kapacitné siete si treba uvedomiť jeden zásadný rozdiel medzi zdrojom EMN a kondenzátorom – celkový elektrický náboj zdroja EMN sa rovná nule, na jeho svorkách je však nenulové napätie, ktoré v galvanickom zdroji zaisťujú elektrochemické pochody, v jednosmerných a striedavých generátoroch je to zvonku vykonaná práca (napr. otáčanie rotora generátora) a zdroj nemožno rozdeliť na jeho kladnú a zápornú polovicu, ako je to v kondenzátore. Na nabitom kondenzátore je síce celkový náboj tiež rovný nule, ale tu rovnako veľké kladné a záporné náboje sú striktne rozdelené na dvoch jeho elektródach. Inač povedané – vnútorný odpor ideálneho zdroja EMN je nulový, zatiaľ čo odpor ideálneho kondenzátora je nekonečný.

      Prvé pravidlo, ktoré možno využiť pri analýze danej siete s kondenzátormi, je v podstate zákon zachovania elektrického náboja, presnejšie skutočnosť, že na nenabitom vodivom telese sa celkový indukovaný náboj rovná nule. "Nenabitým vodivým telesom“ v kapacitnej sieti je vodivé spojenie dvoch, alebo viac elektród kondenzátorov v uzle (napríklad na obr. 1 je to časť siete uzavretá čiarkovaným obdĺžnikom - 3 elektródy troch kondenzátorov), pričom v ceste vodivého spojenia môžu byť aj zdroje EMN (v danom prípade jeden zdroj U_0i), pretože jeho celkový kladný aj záporný náboj sa rovná nule. Pre účely analýzy možno takéto zdroje nahradiť skratmi. Na jednotlivých elektródach kondenzátorov spojených do uzla sa elektrostatickou indukciou indukujú náboje Q_i. Ak je takto spojených l elektród (l kondenzátorov), potom súčet všetkých indukovaných nábojov na elektródach sa rovná nule, teda

                                     
                                            

                                                                                      Obr. 1

kde Q_i = U_iC_i je indukovaný náboj na elektróde i-teho kondenzátora, U_i je napätie príslušného kondenzátora a C_i je jeho kapacita. Tieto náboje alebo napätia treba pri analýze vypočítať.

        Na rovnicu (1) existuje ešte jeden zaujímavý pohľad, ktorý potvrdzuje jej principiálnosť. Napätie na i-tom kondenzátore je U_i = E_id_i, kde E_i je intenzita elektrického poľa v kondenzátore a d_i je vzdialenosť jeho elektród. Kapacita i-teho kondenzátora je C_i = ê₀S_i/d_i (ê₀ = elektrická konštanta - permitivita vákua), kde S_i je efektívna plocha elektródy kondenzátora (predpokladáme, že d_i je podstatne menšie ako ktorýkoľvek rozmer plochy S_i). Dosadením týchto vyjadrení do (1) dosta­neme zaujímavý vzťah

                                                                  E₁S₁ + E₂S₂ +…+ E_iS_i +…+ E_lS_l = 0,

ktorý hovorí, že súčet parciálnych tokov intenzity poľa cez jednotlivé kondenzátory zapojené v uzle sa rovná nule. Je to vlastne Gaussov zákon,  podľa ktorého súčet príspevkov tokov E_iS_i cez vhodne vybranú uzavretú plochu, ktorá „obaľuje“ l elektród kondenzátorov zapojených v uzle sa rovná nule, pretože „obalený“ náboj všetkých uvažovaných elektród sa rovná nule. Na základe týchto úvah možno formulovať:

        Prvé pravidlo (pravidlo uzlov): Algebrický súčet všetkých nábojov elektród kondenzátorov Q_i = U_iC_i  spojených v jednom uzle sa rovná nule.

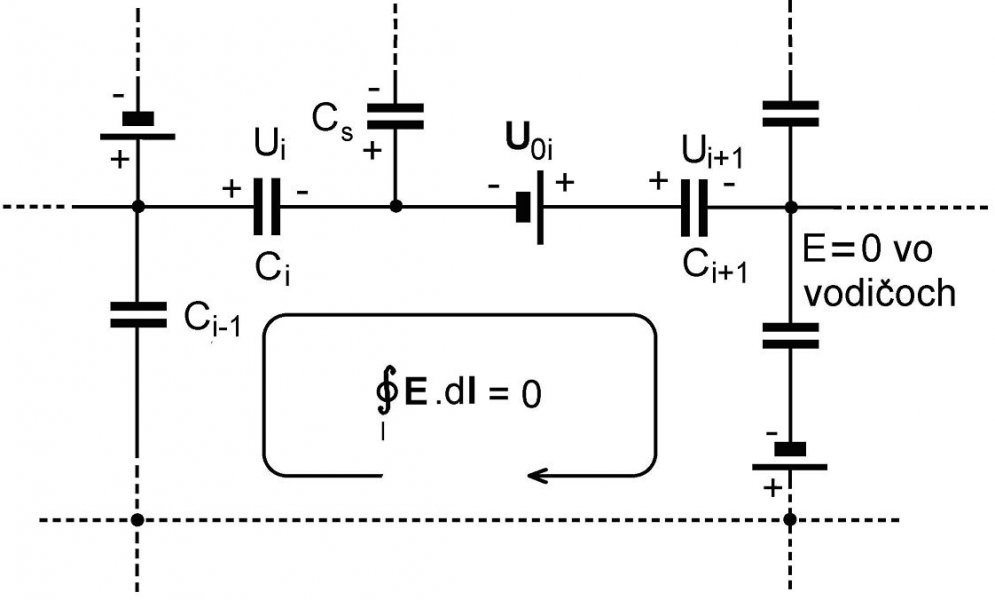
          Druhé pravidlo (pravidlo slučiek):

      Jedna z dvoch Maxwellových rovníc, ktoré platia v elektrostatike tvrdí, že integrál intenzity elektrického poľa po uzavretej dráhe (v slučke) sa rovná nule. Na obr. 2 je zobrazená časť kapacitnej siete, v ktorej orientovaná uzavretá dráha vo vybranej slučke prechádza zdrojmi známych elektromotorických napätí U_0i (k = 1, 2, …, p), známymi kapacitami kondenzátorov C_i (i = 1, 2, …, m) a spojovacími vodičmi (v ktorých sa intenzita elektrického poľa rovná nule).

      Ak Maxwellova rovnica má platiť, potom aj súčet všetkých napätí v slučke sa musí rovnať nule. Na každom nabitom kondenzátore C_i je veľkosť intenzity elektrického poľa E_i = U_i /d_i,  ktorá je kolmá na elektródy S_i, a tie sú vo vzdialenosti d_i. Na jednotlivých kondenzátoroch sú teda neznáme napätia U_i = E_id_i, resp. neznáme náboje Q_i = C_iU_i s neznámou polaritou, (neskôr, pri analýze siete polarity možno zvoliť ľubovoľne, pri konečnom numerickom výpočte záporný výsledok znamená, že polarita napätia je opačná). Takýchto neznámych napätí v slučke je m (m kondenzátorov).

                                               

                                                                                        Obr. 2

      V uvažovanej slučke okrem toho pôsobí aj k zdrojov EMN so známymi napätiami U_0i a známou polaritou (ktoré sú príčinou zatiaľ neznámych napätí na kondenzátoroch). Výsledné EMN týchto zdrojov je algebrický súčet jednotlivých EMN U_0i. Toto napätie sa rovná celkovému algebrickému súčtu napätí U_i = Q_i/C_i na m kondenzátoroch, teda

                                                                        U₀₁+U₀₂+ … +U_0i+…+U_0k-1+U_0k =

                                                      = Q₁/C₁+ Q₂/C₂ +…+ Q_i/C_i +…+ Q_m-1/C_m-1 + Q_m/C_m .                                     (2)

         Tvrdenie, že integrál intenzity elektrického poľa po uzavretej dráhe v obvode zloženom z kondenzátorov a zdrojov sa rovná nule, je vyjadrené vzťahom (2). V slovnom vyjadrení možno sformulovať druhé pravidlo (pravidlo slučiek) takto: 

          Druhé pravidlo (pravidlo slučiek): Algebrický súčet elektromotorických napätí zdrojov U_0i v slučke sa rovná algebrickému súčtu napätí U_i = Q_i/C_i na kondenzátoroch v danej uzavretej slučke.

*****

        Sústavy rovníc typu (1) a (2) umožňujú analýzu akéhokoľvek zapojenia kondenzátorov a zdrojov EMN v elektrickej sieti. Pre účely našej analýzy sú uzlami v sieti miesta, v ktorých sú spojené vždy najmenej tri vetvy. Uzol s dvoma vetvami (s dvoma elektródami) je degenerovaný, pretože poskytuje jedinú informáciu, že príslušné spojené elektródy majú rovnako veľký náboj opačného znamienka. Ak sieť s p uzlami obsahuje zdroje so známymi elektromotorickými napätiami a n známych kondenzátorov, potom analýzou siete treba nájsť n napätí U_i, alebo n nábojov Q_i = C_iU_i na jednotlivých kondenzátoroch. Pri tejto analýze treba zostaviť n lineárne nezávislých rovníc typu (1) a (2). Vhodný spôsob výberu rovníc je nasledovný: 

         Ak sieť obsahuje p uzlov, potom pre p -1 uzlov možno napísať p -1 rovníc typu (1). Rovnica pre p-tý uzol je lineárna kombinácia predchádzajúcich  p -1 rovníc a nepatrí do systému. V sieti možno nájsť m nezávislých slučiek (podobných ako na obr. 2), pričom žiadna z nich nepozostáva iba z už vytvorených slučiek (ináč povedané – každá zo slučiek musí obsahovať aspoň jednu vetvu, ktorá nie je v žiadnej predchádzajúcej slučke). Pre týchto m slučiek možno napísať m rovníc podľa (2), ktoré sú lineárne nezávislé, t. j. také, že žiadna z nich nie je lineárnou kombináciou ostatných. V teoretickej  elektrotechnike sa dokazuje, že počet rovníc potrebných pre analýzu je práve m + p – 1 = n.

      Upozorňujem, že presne rovnaký spôsob výberu uzlov a nezávislých slučiek platí aj pre odporové siete, riešené Kirchhoffovými zákonmi.  Okrem toho, ak sa jednosmerné  zdroje EMN  nahradia striedavými s frekvenciami  f, s nulovým vzájomným  fázovým posuvom, potom z kapacít C_i sa  stanú  kapacitné reaktancie  1/(2pifC_i) a v sieti sa  hľadajú amplitúdy prúdov  alebo ich efektívne hodnoty.

        Z matematického hľadiska daná úloha vedie na riešenie sústavy lineárnych algebrických rovníc pre neznáme U_i  alebo Q_i = C_iU_i. Nemusíte sa obávať – ak sa Vám správne podarí zostaviť n nezávislých rovníc, dnes existujú počítačové programy (napr. „Derive“), ktoré umožňujú analyzovať takéto úlohy v symbolickej forme. Pri zložitých sieťach je najväčší problém zostaviť správne n nezávislých rovníc (tento problém je rovnaký aj pre odporové a impedančné siete). Elektrotechnici vymysleli niekoľko metód na správny výber nezávislých rovníc (známa je metóda úplného stromu). V učebnici „Elektromagnetizmus“, v odseku 3.6 je opísaným spôsobom analyzovaný kapacitný mostík s piatimi kondenzátormi (je potrebných 5  rovníc – 2 rovnice pre p = 2 uzly a 3 rovnice pre m = 3 nezávislé slučky). Ešte jednoduchší je kapacitný delič (1 rovnicu pre slučku a jeden degenerovaný uzol). Pripomínam, že napríklad jednoduché vzorce pre spájanie kondenzátorov (sériové a paralelné) sú triviálnou aplikáciou uvedených pravidiel. Želám Vám príjemný deň! Autor

  PS: Dnes by som sa ešte chcel poďakovať môjmu priateľovi Ivanovi K. z FMFI UK, ktorý bol ochotný strácať čas diskusiou o zvolených témach (úvahách), brzdil ma pri mojich "úletoch" a kontroloval moju gramatiku! Ivan, teda ďakujem! Autor    

 1.8.2008