Elektromagnetické javy a ich miesto v elektronike

úvaha 21-25 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
OBSAH
21. Zákon elektromagnetickej indukcie a teória relativity
22. Maxwellov posuvný prúd a elektromagnetické vlny
23. Meranie rýchlosti svetla
24. Maxwellove rovnice a klasická elektrodynamika
25. Po roku!
_____________________________________________________________________________
21. Zákon elektromagnetickej indukcie a teória relativity

Michael Faraday Vyobrazenie dvoch cievkových systémov,
(1791 – 1867) pomocou ktorých Faraday objavil zákon elektromagnetickej
indukcie. Hore je dvojica cievok na železnom prstencí – predchodca transfornátora.Dole sú dve valcové cievky na
železnom valcovom jadre – ako predchodca induktora
Zákon elektromagnetickej indukcie je jeden z najzávažnejších fyzikálnych zákonov, ktorého objav viedol - v najširšom slova zmysle - k technickej revolúcii. V roku 1831 vykonal anglický učenec Michael Faraday sériu pokusov na jednoduchom zariadení, ktoré je schematicky znázornené na obr. 1. Na železnom prstenci sú navinuté dve cievky: primárna a sekundárna . K primárnej je cez spínač S pripojený zdroj EMN U0 . Faraday na zariadení chcel dokázať, že tak ako elektrický prúd vytvára magnetické pole (čo dokázal niekoľko rokov skôr jeho súčasník, francúzsky fyzik A. M. Ampère), tak magnetické pole vytvorí v sekundárnej cievke elektrický prúd. V zapojení na obrázku čakal, že zapnutím prúdu spínačom v primárnom obvode v železnom prstenci vznikne magnetický tok a ten v sekundárnom obvode vzbudí elektrický prúd, ktorý zaregistruje galvanometer G (vo Faradayovych experimentoch ako galvanometer slúžila malá dvojitá cievočka so zavesenou magnetkou v jej štrbine).
Obr. 1
Nič také sa nestalo, v sekundári sa prúd neobjavil, ale stalo sa niečo iné. Faraday si všimol, že v okamihu zopnutia spínača magnetka vykonala malú krátku výchylku jedným smerom a pri vypnutí prúdu podobnú výchylku opačným smerom. Z toho Faraday usúdil, že nie magnetický tok spôsobí prúd v sekundárnom obvode, ale jeho časová zmena. Tento okamih možno považovať za zrod veľkého objavu s obrovským praktickým dosahom – objav elektromagnetickej indukcie.
Po uvedenom pozorovaní urobil Faraday množstvo ďalších pokusov na zariadení schematicky znázornenom na obr. 2, v ktorom voľne viazané závity obopínajúce plochy S, alebo ploché cievočky sa môžu vzájomne vzdiaľovať, približovať, posúvať sa priečne, otáčať sa okolo kolmej osi a pod. Ukázalo sa, že nestacionárny prúd v obvode s galvanometrom vznikne pri každej zmene indukčného toku, bez ohľadu na jej príčinu. Príčinou môže byť aj náhrada konštantného zdroj EMN U0 zdrojom časovopremenným, alebo časové zmena odporu R.
Obr. 2 Obr.3
Najzávažnejšia je skutočnosť, že v obvode s galvanometrom môže vzniknúť prúd aj bez prítomnosti primárneho prúdového obvodu. Na obr. 3 je znázornený obvod s galvanometrom v blízkosti ktorého sa pohybuje tyčový permanentný magnet. Aj takýto magnet vytvára časovopremenný indukčný tok rovinou závitu a v závite vznikne elektrický prúd. Všetky uvedené prípady vzniku prúdu v sekundárnom obvode majú jeden spoločný znak a to prítomnosť časovopremenného indukčného toku Fi(t) v sekundárnej cievke, pričom dôvod časovej zmeny toku nie je podstatný.
Na základe týchto pozorovaní Faraday usúdil, že veľkosť indukovaného napätia Uindv závite alebo cievočke, ktoré spôsobuje prúd v obvode je čo do veľkosti rovná rýchlosti časovej zmeny indukčného toku, teda veličine dFi(t)/dt. Výraz pre indukované napätie má tvar
Uind =– dFi(t)/dt.
Tento výraz je jednou z možných matematických formulácií Faradayovho zákona elektromagnetickej indukcie, ktorý možno vyjadriť slovne:
Indukované elektromotorické napätie vo vodivom elektrickom obvode sa svojou veľkosťou rovná časovej zmene indukčného toku plochou ktorú obopína prúdová dráha. Smer pôsobenia elektromotorického napätia je daný Lenzovym zákonom.
Lenzov zákon
Súbežne s Faradayom a nezávisle od neho robil výskumy vedúce k elektromagnetickej indukcii profesor Heinrich Friedrich Lenz (1804 – 1865) na petrohradskej akadémii. Lenzova najväčšia zásluha spočíva v tom, že jasne a jednoznačne vyjadril smer pôsobenia indukovaného napätia v obvode, teda smer, v ktorom potečie indukovaný elektrický prúd. Tento princíp je v podstate vyjadrením platnosti zákona zachovania energie v elektrodynamike a formálne vysvetľuje prítomnosť záporného znamienka v zápise zákona elektromagnetickej indukcie. Lenzov zákon možno sformulovať takto:
Indukovaný prúd v obvode svojím magnetickým poľom pôsobí proti zmene indukčného toku, ktorá ho vyvolala.

Heinrich Friedrich Lenz
(1804 – 1865)
Zákon v uvedenom znení sa vzťahuje na indukovaný prúd, t. j. na uzavretý vodivý obvod (závit). V prípade, ak je obvod otvorený, vyjadruje polaritu (smer pôsobenia) indukovaného napätia. Táto polarita určuje smer prúdu, ktorý by v obvode vznikol, ak by sa obvod uzavrel.
Obr. 4
Preskúmajme bližšie podstatu Lenzovho zákona s využitím ilustrácií na obr. 4a, b. Na obr. 4a je tyčový magnet, ktorého smer indukčných čiar ukazuje palec ruky (porovnaj s obr. 4b) a prsty ruky ukazujú smer prúdu v ekvivalentom solenoide, ktorý by nahradil magnet. Ak sa magnet bude pohybovať smerom k závitu, bude indukčný tok závitom vzrastať a podľa Faradayovho aj Lenzovho zákona musí v závite vzbudiť prúd i, ktorého smer je zrejmý z obidvoch obrázkov. Prúd i vytvorí magnetické pole v závite, ktoré smeruje proti poľu magnetu. Cirkulačný prúd v ekvivalentnom solenoide má opačný smer ako prúd v závite, takže závit musí na magnet (solenoid) pri jeho pohybe pôsobiť odpudivou silou Fm. Zasúvanie magnetu do závitu je teda spojené s prácou vonkajšej sily, pričom sa táto práca premení na teplo v elektrickom odpore závitu. Zákon zachovania energie je pritom splnený.
Na proces vzniku indukovaného napätia a prúdu v závite sa možno dívať aj z hľadiska indukčného toku plochou závitu. Tento tok má tendenciu sa zachovávať, teda ak na začiatku je nulový (vzdialený magnet), bude sa snažiť zostať nulový pri akejkoľvek manipulácii s magnetom a pri približovaní magnetu závit bude cez svoju plochu vytvárať protitok (pozri obr. 4a) ako produkt vlastného prúdu.
Ak sa magnet bude zo závitu vyťahovať, indukčný tok závitom pochádzajúci od magnetu sa začne zmenšovať, to však vyvolá protitok plochou závitu (pole opačné ako na obr. 4a) a následne opačný prúd v závite. Odpudivá sila magnetu a závitu sa zmení na príťažlivú a práca vykonaná pri vyťahovaní magnetu sa znovu premení na teplo v odpore závitu. Pri tejto analýze Lenzovho zákona si možno čitateľ uvedomil, že sme súčasne analyzovali činnosť najjednoduchšieho indukčného stroja, v ktorom sa mechanická práca mení na elektrický prúd a súčasne na teplo.
Kuriózne javy by v systéme magnet – závit vznikli vtedy, ak by Lenzov zákon neplatil, teda ak by vo výraze pre zákon elektromagnetickej indukcie bolo znamienko plus (+). Pri približovaní magnetu k závitu by vznikol závitom indukčný tok v smere toku magnetu (opačne ako na obr. 4a). Tento tok by v závite vyvolal prúd opačného smeru ako na obr.4a,b a magnet by bol do závitu vťahovaný. To by následne viedlo k ďalšiemu zväčšeniu indukčného toku... atď. Vznikla by takto kladná spätná väzba, v dôsledku ktorej by sa systém energeticky zrútil. Zákon zachovania energie by bol v takom prípade porušený.
Takáto je formulácia zákona elektromagnetickej indukcie, založená na experimentálnych pozorovaniach M. Faradaya a H. Lenza, ktorá je v tejto formulácii známa už zo stredoškolskej fyziky. V praxi má tento zákon obrovské využitie. Prakticky celá elektrická energetika je založená na platnosti tohto zákona. Na jeho princípe pracujú generátory elektrickej energie, transformátory všetkých výkonov, elektromagnetické brzdy, elektromagnetický ohrev prostredníctvom vírivých prúdov a mnoho iných zariadení. Čitateľov odporúčam na učebnicu „Elektromagnetizmus“, v ktorej zákonu elektromagnetickej indukcie je venovala celá kapitola 7.
*****
Pozrime sa teraz na problematiku zákona elektromagnetickej indukcie z inej strany. Elektromagnetická indukcia vzniká nielen vo vodivom obvode ale aj v prázdnom priestore, alebo v dielektriku. Tam nemožno definovať elektrické napätie alebo elektrický prúd, pretože na to sú potrebné elektrické náboje. Možno ale zaviesť bodovú indukovanú intenzitu elektrického poľa Eind, ktorá vznikne v dôsledku prítomného magnetického poľa B a ktorá bude silovo pôsobiť na pohybujúce sa elektrické náboje. Treba vyjadriť túto indukovanú intenzitu, a to vlastne bude vyjadrenie zákona elektromagnetickej indukcie vo voľnom priestore, kde netečú prúdy.

Hendrik Antoon Lorentz
(1853 -1928)
Takúto formuláciu zákona elektromagnetickej indukcie predložil holandský fyzik Hendrik Antoon Lorentz (1853 -1928), keď v roku 1909 publikoval významnú teoretickú štúdiu o elektróne (Lorentz H. A.: The Theory of Electron, New York 1909). Tam Lorentz uviedol výraz pre silu Felmag, ktorou elektromagnetické pole E a B pôsobí na bodový náboj q (napríklad na elektrón), ak sa v ňom náboj pohybuje rýchlosťou v.Táto sila má tvar
Felmag = q(E + v ×B).
Sila sa nazýva Lorentzovou silou a skladá sa z dvoch časti: zo známej elektrickej Coulombovej sily qE, kde E je intenzita elektrického poľa od všetkých, iných nábojova zmagnetickej sily qv × B, ktorá ma zrejme relativistický charakter, pretože závisí od rýchlosti. Magnetická indukcia B v mieste náboja q je daná pohybom všetkých iných nábojov.
Je otázkou, aký význam vo výraze pre magnetickú silu má vektorový súčin v × B? Rozmer tohto súčinu je V/m, teda má rozmer intenzity elektrického poľa, o čom sa možno presvedčiť rozmerovou analýzou. Hľadaná indukovaná intenzita elektrického poľa je teda
Eind = v × B
a tú náboj „vníma“ ak sa v magnetickom poli pohybuje rýchlosťou v.
Vzniká tiež otázka, kde Lorentz zobral túto intenzitu. Tí čitatelia, ktorí v učebnici „Elektromagnetizmus“ čítali kapitolu 6.5: Lorentzove transformácie elektromagnetických polí, si možno spomenú na všeobecné relativistické transformačné vzťahy pre elektromagnetické polia, ktoré platia pri prechode pozorovateľa (v našom prípade pozorovateľom je náboj q) z pevnej, do pohyblivej (čiarkovanej) sústavy – sú to tam uvedené výrazy (6.125). Ak rýchlosť pohyblivej sústavy v « c, potom priečne zložky polí E´ a B´ (priečne k pohybu sústavy) vo výrazoch (6.125) v pohyblivej sústave prejdú na tvar
E´ = E + v × B,
B´ = B – v/c2 × E.
Všimnime si najprv prvý výraz. Je to presne tá istá intenzita E´, ktorá v Lorentzovom výraze pre silu pôsobí na náboj q, teda intenzita elektrického poľa z pevnej sústavy E a indukovaná intenzita Eind = v × B.
Že indukovaná intenzita je kompatibilná s indukovaným napätím podľa všeobecne známeho výrazu uvedeného na začiatku tejto úvahy dokážeme tak, že necháme na elementárny kúsok prúdovodiča dĺžky dl pôsobiť intenzitu Eind. Na pohybujúcom sa prúdovodiči v magnetickom poli B rýchlosťou v vznikne elementárne napätie dUind = (v ×B)·dl (ak vektory v, B a dl sú navzájom na seba kolmé, potom dUind = vBdl). Predpokladajme, že dl je elementárny oblúčik sekundárneho závitu S na obr. 2, ktorý nech sa teraz pohybovať (samozrejme s celým závitom) priečne, k osi závitov, rýchlosťou v. Ak sčítame elementárne napätia oblúčikov pozdĺž celého závitu, dostaneme výsledné indukované napätie v závite
Uind = Dráhový integrál po uzavretej dráhe príspevkov [(v × B)·dl].
Tento výraz v nás možno nevzbudzuje dôveru, že udáva to isté indukované napätie v závite, ktoré sme už dostali na začiatku našej úvahy, ako časovú zmenu indukčného toku Fi(t). Je azda toto napätie iné? Potom by ale naše posledné úvahy mohli byť aj chybné! Môžete byť spokojní – je to to isté napätie, len teraz je zdôvodnené pohybom závitu v magnetickom poli a nie zmenou magnetického indukčného toku. Že je to skutočne tak, dôkaz nájdete v odseku 7.3 viackrát citovanej učebnice.

Einstein a Lorentz
pred Ehrenfestovym domom v Leidene v roku 1921
Čo povedať na záver našej úvahy o elektromagnetickej indukcii? Tvrdím, že tento zákon je jeden z najkrajších zákonov klasickej fyziky. Udivuje svojou variabilitou prejavov a nespočetnými možnosťami dôležitých praktických aplikácii. K jeho teoretickému zdôvodnenie viedla však až teória relativity.
*****
Z Lorentzovych transformácii elektromagnetických polí nám zostal ešte jeden výraz, ktorému tu, kvôli kontinuite, treba venovať aspoň niekoľko slov. Je to výraz pre magnetickú indukciu B´ v pohybujúcej sa sústave. Ak v « c, potom táto indukcia
B´ = B – v/c2 × E.
Ako vidieť, aj magnetická indukcia v pohyblivej sústave sa skladá z dvoch častí: z obyčajnej indukcie B v pevnej sústave a zo "záhadnej" časti – v/c2 ×E, pre ktorú môžeme napísať vyjadrenie
– v/c2 ×E = –µ0epsilon0v× E=–µ0 Hpos
kde µ0 a epsilon0 sú magnetická a elektrická konštanta (permeabilita a permitivita voľného priestoru) a
Hpos = epsilon0v× E=v× D
je intenzita nestacionárneho magnetického poľa, ktoré súvisí s elektrickým poľom (E, D) a s posuvným prúdom, ktorý bez experimentálneho dôkazu zaviedol do elektromagnetickej teórie jej tvorca J. C. Maxwell v rokoch 1864 až 1973. Z výrazu plynie, že elektrické pole môže byť príčinou vzniku magnetického poľa a s ktorým priamo súvisí posuvný prúd, ktorý sa tiež nazýva Maxwellov posuvný prúd. Tento prúd svojimi experimentmi, asi o dvadsať rokov neskôr, dokázal nemecký fyzik H. Hertz
James Clerk Maxwell
(1831 – 1879)
Keďže problematika posuvného prúdu sa z analyzovanej problematiky vymyká, túto úvahu ukončíme a snáď nabudúce... Za trpezlivosť ďakujem a želám krásny deň! Autor
19.11.2008
22. Maxwellov posuvný prúd a elektromagnetické vlny
Hans Christian Oersted André Marie Ampère
(1777 – 1851) (1775 – 1836)
O magnetizmus sa intenzívne začal zaujímať francúzsky učenec André Marie Ampèr, ktorý vykonal množstvo experimentov súvisiacich s magnetickým silovým pôsobením elektrických prúdov. Na základe týchto pozorovaní Ampère sformuloval niektoré zákonitosti, z ktorých najznámejšie sú „Ampérov silový zákon“, alebo „Ampérovo pravidlo pravej ruky“. Po Ampérovi bol nazvaný aj jeden zo základných zákonov elektromagnetizmu (jedna zo štyroch Maxwellovych rovníc), ktorý pre stacionárne magnetické pole v matematickej formulácii znie veľmi jednoducho a síce (pozri „Elektromagnetizmus“, odsek 6.1.6) , že: t. j. že dráhový integrál magnetických príspevkov H.dl po uzavretej dráhe sa rovná celkovému obopnutému prúdu elektrických nábojov I (nemýliť s Ampérovym silovým zákonom), jednoducho povedané – magnetické pole je produktom prúdu elektrických nábojov.
James Clerk Maxwell
(1831 – 1879)
V šesťdesiatych rokoch devätnásteho storočia anglicky fyzik James Clerk Maxwell pri tvorbe všeobecnej elektromagnetickej teórie podrobil rovnicu (1) kritike a usúdil, že je neúplná. Maxwell vyhlásil, že tak ako časovopremenné magnetického poľa môže produkovať elektrické pole a tým aj elektrický prúd (čo ukázal Faraday formuláciou zákona elektromagnetickej indukcie – pozri Úvahu 21), tak môže časovopremenné elektrické pole produkovať magnetické pole a to sa na rovnici musí prejaviť. Toto logické tvrdenie však v Maxwellovych časoch nemalo nijakú experimentálnu oporu. Maxwell svoje geniálne tvrdenie vyjadril rovnicou, ktorú dnes píšeme v tvare
Druhý člen na pravej strane tejto rovnice, pridal Maxwell k rovnici (1), ten má, samozrejme, rozmer elektrického prúdu [A]. Maxwell tento prúd nazval posuvným prúdom (displacement current), ktorý sa podieľa na tvorbe magnetického poľa podobne, ako prúd nábojov I. Argumentom pre prítomnosť tohto člena v rovnici je aj skutočnosť, že iba tak je zaručená súčasná platnosť zákona zachovania elektrického náboja (pozri „Elektromagnetizmus“, ods. 6.3). Veličina pod integrálom na pravej strane rovnice
je objemová hustota posuvného prúdu.
Podľa rovnice (2) sa na produkcii magnetického poľa v istom pomere zúčastňujú obidva prúdové hustoty. Vo voľnom priestore, bez prítomnosti nábojov, je magnetické pole závislé iba od dD/dt. Takisto je to v kvalitných dielektrikách, kde pojem „posuvný“ sa spája s posuvom nábojových centier v dielektriku. Naopak, v dobrých vodičoch, je elektrická indukcia D obyčajne malá, a ak jej časové zmeny sú pomalé, posuvný prúd možno zanedbať a magnetické pole je dané iba vodivým prúdom I. V ostatných prípadoch majú obidva prúdy porovnateľný podiel na tvorbe magnetického poľa.
*****
Obr. 1
Pokúsime sa teraz Maxwellov predpoklad o existencii posuvného prúdu dokázať mysleným experimentom. Na obr. 1 je znázornený jednoduchý obvod pozostávajúci z kondenzátora C a rezistora R. Kondenzátor pozostáva z prehnane rozmerných, ideálne vodivých dosiek, s čelnou plochou S0 uložených v istej vzdialenosti. Celý elektrický odpor obvodu je sústredený v rezistore R. V čase t = 0 je na kondenzátore nejaký celkový náboj ±Q0 a zopne sa spínač P. V obvode začne tiecť časovo premenný, exponenciálne zanikajúci prúd I s časovou konštantou RC (pozri „Elektromagnetizmus“, odsek 5.8)
kde Q(t) = S0sigma(t) je okamžitý náboj na kondenzátore a sigma(t) je okamžitá plošná hustota náboja na čelných plochách kondenzátora (charakter časovej závislosti pre naše úvahy nie je podstatný). Prúd v obvode vytvorí v celom priestore, v prúdovodičoch a okolo nich, v masívnych doskách (predpokladáme, že nie sú feromagnetické), aj v priestore medzi doskami kondenzátora magnetické pole, ktoré bude s časom takisto zanikať. Vytvorme okolo prúdovodiča uzavretú dráhu l v tvare kružnice a položme si otázku: čím je daná hodnota integrálu H.dl po uzavretej dráhe l? Podľa výrazu (1) je jeho hodnota daná celkovým obopnutým prúdom, presnejšie tým prúdom, ktorý preteká plochou S napnutou na čiaru l. Lenže na plochu S sa v Ampérovom zákone nekladie nijaká podmienka, to znamená, že takých plôch je ľubovoľné množstvo. Môže to byť kruhová šrafovaná rovinná plocha S1, ktorou prechádza prúdovodič, alebo plocha S2 prechádzajúca masou dosky kondenzátora, ale nie je vylúčená ani plocha S3, prechádzajúca vnútrom kondenzátora (plocha ako pančucha obaľuje pravú dosku kondenzátora), ale tú žiadny vodivý prúd nepretína. Plochami S1 a S2 tečie rovnaký prúd I = dQ/dt = S0dsigma/dt.
V treťom prípade plochou S3 musí tiecť veličina, ktorá s plošnou hustotou náboja sigma priamo súvisí. V dutine kondenzátora je elektrická indukcia D = sigma, rovná plošnej hustote náboja na čelách kondenzátora, takže plochou S3 tečie veličina
Toto je zrejme prúd, ktorý je daný druhým členom na pravej strane rovnice (2), pričom prvý člen je nulový. Treba si všimnúť, že zatiaľ čo vektor D smeruje sprava doľava (od kladnej elektródy k zápornej), dD/dt smeruje naopak, pretože prúd I, plošná hustota náboja sigma a tým aj vektor elektrickej indukcie D s časom klesajú (vybíjaný kondenzátor). Posuvný prúd S0dD/dt má teda rovnaký smer, ako prúdu kladných nábojov v obvode. Možno povedať, že vodivý prúd vo vodičoch a v rezistore sa uzatvára posuvným prúdom v prázdnom priestore (alebo v dielektriku) kondenzátora.
Hodnota integrálu H.dl po uzavretej dráhe l vo výraze (2) môže byť skutočne daná buď integrálom prúdovej hustoty vodivého prúdu J = dsigma/dt vo vodičoch, alebo prúdovej hustoty posuvného prúdu Jp = dD/dt v dielektriku alebo vo voľnom priestore (vo vákuu). Ak tieto prostredia nie sú oddelené, ako už bolo povedané, potom sa na tvorbe integrálu podieľajú súčasne obidva prúdy, tak ako to stanovuje rovnica (2). Treba nakoniec povedať, že uzavretá dráha l môže ležať aj v štrbine kondenzátora, rovnica (2) platí aj vtedy.
*****
Nahraďme teraz rezistor v zapojení na obr. 1 cievkou s indukčnosťou L, vznikne obvod podľa obr. 2 a zopnime spínač P. Kladné náboje z pravej elektródy neprejdú okamžite na zápornú elektródu, ale v dôsledku samoindukcie cievky L v obvode vznikne časovo premenný elektrický prúd I, ktorý je na začiatku nulový, pretože na cievke je protinapätie veľkosťou rovné napätiu na kondenzátore. Prúd I stúpa v smere ako je to zobrazené šípkou na obrázku, protinapätie UL klesá, až klesne na nulu. V tom okamihu prúd v cievke dosahuje maximálnu hodnotu (maximálne je aj magnetické pole v cievke) a na doskách kondenzátora je nulový náboj. Medzi doskami je teraz nulové elektrické, ale maximálne magnetické pole, pretože časová zmena elektrického poľa dD/dt, teda posuvný prúd, sú v tomto okamihu maximálne, vektor D je nulový a mení polaritu a vektor –dD/dt v kondenzátore smeruje doprava.
Obr. 2
V tom čase nahromadená magnetická energia cievky núti prúd tiecť stále rovnakým smerom, pričom prúd začne klesať. Napätia na cievke aj na kondenzátore, teraz v opačnom smere, stúpajú na maximálnu hodnotu. V okamihu keď napätia sú maximálne, prúd cievkou, aj posuvný prúd v kondenzátore sú nulové, a nulové sú aj obidve magnetické polia. Kondenzátor je plne nabitý, ale s opačnou polaritou, elektrické pole v kondenzátore je maximálne!
Proces pohybu nábojov môže teraz prebiehať netlmene (za predpokladu, že v obvode nie sú žiadne straty energie), teraz znovu opačným smerom. Systém je vlastne kmitavý LC obvod, v ktorom si možno všimnúť, že medzi doskami kondenzátora existuje periodické elektrické – ale čo je dôležité – aj periodické magnetické pole. Prvé je dané vektorom E = D/epsilon a druhé vektorom H, závislým od dD/dt. Tieto polia v kondenzátore kmitajú s frekvenciou f = 1/(2pi(LC)(1/2)), pi = 3,14159..... je Ludolfovo číslo. Ako vidieť, sú posunuté vo fáze o pi/2 = 900 (jedno pole je maximálne, druhé je nulové), čo je známe aj z analýzy kmitov LC obvodov v teórii striedavých prúdov (pozri napr. úvahu 17).
Vráťme sa v mysli k našej prvej úvahe, v ktorej sme vyjadrili presvedčenie, že v prírode existuje iba jeden zdroj elektromagnetického poľa v svojich dvoch podobách, a to kladné a záporné elektrické náboje, a že neexistujú žiadne magnetické náboje. Tento nedostatok symetrie v zdrojoch poľa je tu vykompenzovaný prekrásnou symetriou elektromagnetických polí, ktorá sa prejavuje v tom, že:
Každá časová zmena magnetického poľa vedie k vzniku elektrického poľa a naopak, každá časová zmena elektrického poľa vedie k vzniku magnetického poľa. Najdôležitejším dôsledkom tejto symetrie sú elektromagnetické vlny.
*****
Počas kmitov obvodu „otvorme“ teraz kondenzátor tak, že vyvrátime jeho dosky na opačné strany indukčnosti, ako na obr. 3. Útvar ktorý vznikne, je predobraz žiarivého elektrotechnického dipólu (v praxi ho obyčajne predstavuje v strede budená kovová tyčka – Hertzov dipól o celkovej dĺžke rovnej dĺžke polvlny budených kmitov), ktorý sa používa ako prijímacia alebo vysielacia anténa elektromagnetických vĺn.
Heinrich R. Hertz
(1857 – 1894)
Elektromagnetické pole, ktoré bolo predtým uzavreté v kondenzátore, sa teraz vo forme elektromagnetickej vlny vyžiari rýchlosťou svetla do vonkajšieho priestoru. V uvažovanom prípade celý jav bude trvať veľmi krátko, pretože energia elektromagnetického poľa sa rýchlo rozptýli do priestoru, náboje na doskách sa neutralizujú a kmity v systéme ustanú. Na udržanie kmitov by sa systém musel z vonku budiť.
Obr. 3 Obr. 4: Pôvodne Hertzovo zapojenie
na vysielanie a príjem
elektromagnetických vĺn
Treba povedať, že pred otvorením kondenzátora bolo elektromagnetické pole uzavreté vo vnútri štrbiny kondenzátora, elektromagnetický výkon sa von nevyžaroval (alebo ak, tak iba veľmi málo) a obvod mohol kmitať veľmi dlho.
Elektromagnetické vlny sa môžu rôznym spôsobom spracovávať (napr. modulovať, detegovať a i.) a po prechode voľným priestorom znovu prijímať a spracovať.
Maxwell predpovedal existenciu elektromagnetických vĺn v roku 1864 v práci: Maxwell, J. C., Phil. Magazine 155 (1864). Elektromagnetické vlny krátko po vzniku Maxwellovej elektromagnetickej teórie objavil v roku 1887 experimentálne nemecký fyzik H. Hertz (pozri obr. 4) na Univerzite v Karlsruhe a opísal ich v práci: Kräfte elektrischer Schwingungen behandelt nach Maxwellschen Theorie, Ann. d. Physik (1888).
Nech Vám dnešný deň prinesie veľa dobrého! Autor
30.11.2008
23. Meranie rýchlosti svetla
E io rispondo: Io credo in uno Dio
solo ed etterno, che tutto ´l ciel move,
non moto, con amore e con disio;
e a tal creder non ho io pur prove
fisice e metafisice, ma dalmi
anche la verità che quinci piove ...
Dante Alighieri: La Divina Commedia, Paradiso: Canto XXIV, 130-135
Nuž vravím: Verím v jediného Boha
a večného, čo hýbe nebo celé,
sám nehnutý – tak plá v ňom láska mnohá!
K tej miere nielen Fyzika mi stelie
s Metafyzikou dôkazy; ich dal mi
i pravdy jas, čo prší v božskom diele ... Preklad: Viliam Turčány, 1986
Meranie rýchlosti svetla patrí medzi základné úlohy experimentálnej fyziky, pretože je skúšobným kameňom platnosti Maxwellovej elektromagnetickej teórie a Einsteinovej teórie relativity, odhliadnuc od praktických potrieb poznania rýchlosti svetla.
Správnejšie by táto úvaha mala niesť názov "meranie rýchlosti šírenie elektromagnetických vĺn", pretože to, čo nazývame "rýchlosťou svetla vo vákuu", je v skutočnosti univerzálna prírodná rýchlostná konštanta, ktorá udáva rýchlosť šírenia signálov v celom frekvenčnom pásme elektromagnetického spektra. Táto rýchlosť je nezávislá od frekvencie a má rovnakú hodnotu v každej vzťažnej sústave, nie je teda v pravom zmysle kinematickou veličinou. Ak ju nazývame "rýchlosťou svetla", robíme tak z historických dôvodov, pretože jej prvé merania boli urobené v tom pásme elektromagnetického spektra, ktoré vníma ľudské oko a to vtedy, keď o elektromagnetických vlnách sa ešte ani nechýrovalo.

Galileo Galilei
(1564 - 1642)
Dávno pred Maxwellom a Einsteinom si otázku o rýchlosti svetla položil taliansky učenec Galileo Galilei, ktorý sa okolo roku 1600 pokúsil rýchlosť svetla aj zmerať ako pomer svetlom prejdenej dráhy s a na to potrebného času t. Pri Galileových technických možnostiach je len samozrejmé, že takýto pokus skončil neúspechom. Aj Galileovi bolo jasné, že na meranie takýchto nevídaných rýchlostí treba spoľahlivo merať veľmi veľké vzdialenosti a veľmi krátke časové intervaly. Bolo teda len logické očakávať od astronómie, že bude tou vedou, ktorá poskytne vhodné metódy na meranie rýchlosti svetla. V roku 1675 dánsky astronóm žijúci v Paríži Olaf Römer na základe pozorovania zatmení Jupiterových mesiacov stanovil rýchlosť svetla na hodnotu 2.108m.s–1. O päťdesiat rokov neskôr anglický astronóm James Bradley ju stanovil úplne inou metódou na 3.108m.s–1.
V roku 1849 francúzsky fyzik Armand Hipolyte Louis Fizeau (1819 – 1896) zmeral rýchlosť svetla nie astronomickou metódou. Fizeauova aparatúra na meranie rýchlosti svetla je znázornená na obr. 1. Svetlo zo zdroja po odraze na polopriepustnom zrkadle prechádza prvou šošovkou. Za šošovkou v jej ohniskovej rovine 0 rotuje ozubený kotúč s počtom zubov N, ktorého kruhovú frekvenciu omega = 2×pi×f možno meniť (pi = 3,14159..... je Ludolfovo číslo, f je frekvencia). Kotúč "rozseká" svetelný zväzok na sled svetelných zábleskov, ktoré rýchlosťou c prekonávajú dráhu l (vo Fizeauových pokusoch 8630 m) k zrkadlu a späť ku kotúču. Ak sa zvolí kruhová frekvencia otáčok kotúča tak, že za čas potrebný na prelet záblesku k zrkadlu a späť sa koleso pootočí tak, že nasledujúci zub záblesk zatieni, pozorovateľ neuvidí žiadne odrazené svetlo a obraz zdroja zmizne z jeho zorného poľa. Je zrejmé, že zatemnenie zorného poľa nastane vtedy, ak sa za uvedený čas kotúč pootočí o uhol theta = pi/N. Z podmienky rovnakého času potrebného na prelet svetla po dráhe 2l a pootočenia kotúča o uhol theta plynie, že
theta/omega = 2×l/c
z čoho rýchlosť svetla
c = 2×omega×l / theta = 4lfN
Kotúč vo Fizeauovom experimente mal N = 720 zubov a otáčal sa s frekvenciou f = 12,6 Hz. Zo posledného vzťahu plynie pre rýchlosť svetla hodnota 3,13.108 m.s–1, čo je hodnota asi o 5 % väčšia ako poskytujú súčasné merania. Chyba merania je spôsobená hlavne nepresnosťou stanovenia okamihu zatemnenia zorného poľa.
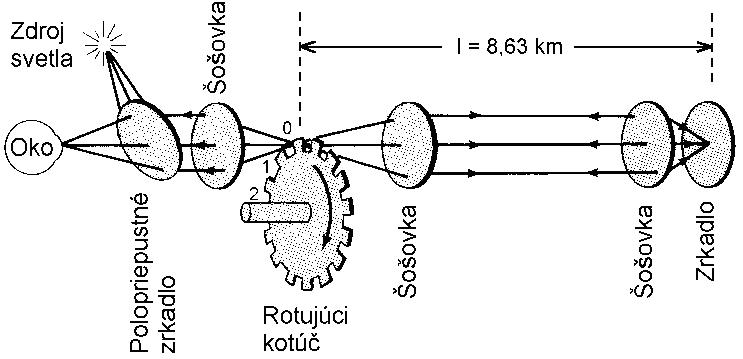
Obr. 1
Fizeauov experiment zdokonalil v roku 1862 francúzsky fyzik Jean Bernard Léon Foucault (1819 – 1868) tým, že rotujúci kotúč nahradil rotujúcim zrkadlom. Metódou rotujúceho zrkadla vykonal v rokoch 1878 až 1930 mnoho meraní rýchlosti svetla známy americký fyzik Albert Abraham Michelson (1852 – 1931), ktorý v roku 1926 stanovil rýchlosť svetla na hodnotu 299 796 km.s–1 s neistotou ± 4 km.s–1. Nie je nezaujímavé uviesť, že Michelsonovi sa metódou rotujúceho zrkadla podarilo zmerať 35 kilometrovú vzdialenosť vrcholov kalifornských hôr Mount Wilson a Mount San Antonio s presnosťou lepšou ako ± 2,54 cm (± 1 inch).
Michelsonovu metódu modifikoval v roku 1950 švédsky fyzik Bergstrand, ktorý nahradil rotujúce zrkadlo elektronickým zariadením pozostávajúcim z pulzného zdroja a detektora. Zmenou frekvencie pulzov možno dosiahnuť maximum údaja detektora. Zariadenie má komerčný názov geodimeter a pomocou neho bola určená hodnota rýchlosti svetla (299 792,7 ± 0,25) km.s–1. Geodimeter sa dnes používa na rutinné merania veľkých vzdialeností na základe známej rýchlosti svetla.
Všetky doteraz uvedené metódy sa zakladajú na meraní dĺžok a času a sú použiteľné skutočne iba na meranie rýchlosti svetla. Oveľa presnejšie výsledky merania poskytujú metódy založené na pozorovaní stojatých vĺn, pri ktorých sa experimentálne určuje vlnová dĺžka lambda vo voľnom priestore a frekvencia f elektromagnetickej vlny. Rýchlosť svetla sa potom vypočíta zo známeho vzťahu
c = lambda×f
Vlnové dĺžky a frekvencie sa dnes merajú s vysokou presnosťou v celom elektromagnetickom pásme a presnosť stúpa s frekvenciou. Na určenie dĺžky vlny ako dvojnásobnej vzdialenosti medzi minimami stojatej vlny sa používajú rôzne druhy interferometrov resp. rezonátorov, ktoré majú rôzne konštrukcie podľa použitej frekvencie.
Prvé merania rýchlosti c na rádiových frekvenciách vykonal J. Mercier (Franc.) v roku 1924 meraním stojatých vĺn na dvojvodičových vedeniach opísaných napr. v knihe A. Tirpák: „Elektronika veľmi vysokých frekvencií“, čiastočne aj v knihe A. Tirpák: " Elektromagnetizmus". V mikrovlnovom pásme prvýkrát merali rýchlosť c roku 1950 Essen (Angl.) a dvojica výskumníkov Bol a Hansen (USA). Essen meral rezonančnú vlnovú dĺžku v cylindrickom dutinovom rezonátore na frekvencii
f = 9,498 300.109 Hz
Pre polomer rezonátora R = 3,258 76 cm a jeho dĺžku l = 15,645 74 cm zistil v rezonátore n = 8 pozdĺžnych polvĺn, z čoho stanovil dĺžku vlny v rezonátore na hodnotu
lambdav = 2×l / n = 3,911 44 cm
Dĺžka vlny lambdav v rezonátore súvisí s dĺžkou vlny lambda vo voľnom priestore podľa vzťahu
lambdav = lambda /(1 – (lambda / lambdakr)2)1/2,
kde
lambdakr = 1,639 662 R = 5,343 27 cm
je kritická vlnová dĺžka v cylindrickom prázdnom vlnovode s daným polomerom (pozri A. Tirpák: „Elektronika veľmi vysokých frekvencií“, kap.2, odsek 4 a kap. 4, odsek 4, resp. 8 na tejto webovej stránke). Po dosadení za lambdav a lambdakr do výrazu pre vlnovú dĺžku lambda v neohraničenom voľnom priestore (približne vo vákuu) dostal hodnotu
lambda = 3,15159 cm
Nakoniec pre rýchlosť svetla dospel k hodnote
c = lambda×f = 2,997 814 5.108 m.s–1
Essen vykonal množstvo experimentov za rôznych podmienok a po starostlivom výbere výsledkov uviedol ako najpravdepodobnejšiu hodnotu s udaním neistoty
c = (299 792,5 ± 3) km.s–1
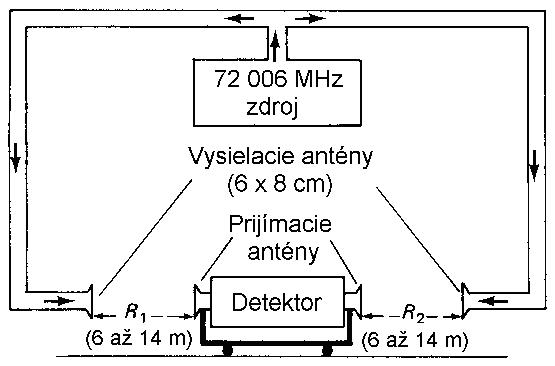
Obr. 2
Mikrovlnový interferometer so štyrmi lievikovými anténami použil v rokoch 1952 až 1958 na určenie c Angličan K. D. Froome najprv na frekvencii f = 25 000 MHz s vlnovou dĺžkou lambda = 1,2 cm a neskôr na frekvencii f = 72 006 MHz s vlnovou dĺžkou lambda = 4,16 mm. Frekvencia bola meraná s mimoriadnou presnosťou metódami mikrovlnovej techniky. Schéma zariadenia na meranie je znázornená na obr. 2. Výkon mikrovlnového zdroja je rozvetvený do dvoch zväzkov, pomocou vlnovodov a lievikových antén vyžiarený z dvoch strán proti detektoru namontovanému na pohyblivom vozíku. Pri pohybe vozíka detektor registruje interferenčné minimá a maximá (vzdialenosť susedných miním je lambda/2), pričom na 8-metrovej dĺžke sa registruje veľký počet vlnových dĺžok, čo značne zvyšuje presnosť merania lambda. Výsledky Froomových meraní viedli k hodnote
c = lambda×f = (299 792,5 ± 0,10) km.s–1
čím sa zlepšila presnosť a precíznosť Bergstrandových meraní.
Najpresnejšie merania rýchlosti svetla boli vykonané v 70-tých rokoch minulého storočia v americkom Národnom úrade štandardov (National Bureau of Standards, Gaithersburg, Maryland) a vo Veľkej Británii v národnom fyzikálnom laboratóriu (National Physical Laboratory). Po Froomových experimentoch bolo fyzikom jasné, že efektívnym spôsobom zvýšenia presnosti merania rýchlosti c je rozšírenie Froomovej metodiky z mikrovlnovej do infračervenej a viditeľnej oblasti elektromagnetického spektra. Presnosť merania c v tom období posunuli výrazne dopredu dva objavy: vysokofrekvenčná spektroskopia a vynález laseru. Tieto vynálezy poskytli frekvenčne veľmi stabilné koherentné zdroje signálov v infračervenej a viditeľnej oblasti a metódy veľmi presného stanovenia frekvencie. Meranie frekvencie sa stalo mimoriadne presným vďaka vývoju céziového (Cs) frekvenčného štandardu s relatívnou presnosťou 10–13. Meranie frekvencie a času vo fyzike patria dnes k najpresnejším meraniam. V roku 1967 stanovila XIII. Generálna konferencia pre miery a váhy novú definíciu sekundy, podľa ktorej:
Jedna sekunda (1 s) je časový interval, ktorý sa rovná 9 192 631 770 periódam elektromagnetického žiarenia emitovaného pri energetickom prechode medzi obidvomi hyperjemnými hladinami základného stavu atómu cézia 133 v nulovom magnetickom poli.
V novembri roku 1983 prijala XVII. Generálna konferencia pre miery a váhy aj novú definíciu jednotky dĺžky – metra, podľa ktorej:
Jeden meter (1 m) je vzdialenosť, ktorú prejde svetlo vo voľnom priestore (vo vákuu) za 1/299 792 458 sekundy.
Vysoká presnosť merania frekvencie a vlnovej dĺžky umožnili vedemdesiatych rokoch 20. storočia spresniť meranie rýchlosti svetla asi stokrát. Céziový štandard umožnil presne merať frekvenciu stabilizovaných klystrónov, generovaných harmoník hrotových diód a Josephsonovských mostíkov a sérií spektrálnych čiar laserov, ako sú
Najpresnejšie autorovi známe merania rýchlosti svetla s využitím stabilizovaných laserov vykonali v roku 1973 Evenson (USA) a i. s nameranou hodnotou rýchlosti svetla
c = (299 792,457 4 ± 0,001 1) km.s–1
a v roku 1974 Blaney (Angl.) a i. s hodnotou
c = (299 792,459 0 ± 0,000 8) km.s–1
Presnosť merania rýchlosti svetla c s odchýlkou iba ±80 cm.s–1, ktorú dosiahol Blaney predstavuje percentuálnu odchýlku iba ±0,000 000 267 % od najpravdepodobnejšej hodnoty, čím sa rýchlosť svetla radí skutočne medzi prírodné konštanty, ktoré sú známe s najvyššou presnosťou.
V roku 1975 na XV. Generálnej konferencii pre miery a váhy na základe starostlivého a kritického posúdenia všetkých známych výsledkov merania bola stanovená rýchlosť svetla vo voľnom priestore na presnú hodnotu
c = 299 792 458 m.s-1.
Táto hodnota dnes slúži za základ definície metra, a je tiež základom na určenie ďalších číselných konštánt v SI-sústave, ako sú elektrická konštanta (starý názov "permitivita voľného priestoru - vákua") epsilon0 = 1/(µ0c2) ~ 8,854.10-12 F.m-1, charakteristická (vlnová) impedancia voľného priestoru Z0 = µ0c ~ 376,730 ohmov (µ0 = 4×pi.10-7H.m-1 je definitoricky daná magnetická konštanta - starý názov "permeabilita voľného priestoru"), pokojové energie elementárnych častíc mc2 a i. Uvedená hodnota c nie je samozrejme definitívna. Ak sa zvýši presnosť merania rýchlosti svetla bude aj táto numerická hodnota podrobená revízii.
Tabuľka: Rýchlosť svetla vo voľnom priestore (vo vákuu)
V tabuľke „Rýchlosť svetla vo vákuu“ sú uvedené vybrané merania rýchlosti svetla vykonané od Galileových dní. Tabuľka je dôkazom veľkosti, vytrvalosti a dômyslu ľudského ducha. Vidieť z nej, ako sa s rokmi zvyšovala presnosť merania, aká široká paleta meracích metód bola pritom využívaná a tiež medzinárodné zastúpenie vedcov na meraní rýchlosti svetla. Po dlhom čase Vám želám pekný a dobrý deň! Autor
26.04.2009
24. Maxwellove rovnice a klasická elektrodynamika
James Clerk Maxwell
(1831 - 1879) ·
Z pohľadu ďalekej budúcnosti ľudstva – povedzme desaťtisíc rokov – bude Maxwellova formulácia zákonov elektrodynamiky hodnotená ako najväčší počin 19. storočia. Americká občianska vojna vedená v tom istom desaťročí bude v porovnaní s touto dôležitou vedeckou udalosťou hodnotená ako bezvýznamná provinciálna šarvátka.
"Feynmanove prednášky z fyziky"
" Formulácia týchto rovníc bola vo fyzike najväčšou udalosťou od Newtonových čias"
Albert Einstein: Evolúcia fyziky
„War es ein Gott, der diese Zeilen schrieb …?“ (Bol to Boh, čo písal tieto riadky … ?)
L. Boltzmann: Prednášky o Maxwellovej teórii
elektriny a svetla, Mníchov 1893.
Maxwellove rovnice sú vrcholným bodom klasickej teórie elektromagnetizmu, pretože v matematickej forme predstavujú základné prírodné zákony, ktoré opisujú elektromagnetické javy. V tejto úvahe budeme sumarizovať výsledky jednotlivých častí elektromagnetizmu, a poukážeme na vzájomné súvislosti, ktoré platia medzi jednotlivými veličinami klasickej elektromagnetickej teórie.
V elektromagnetizme sa definujú štyri vektory elektromagnetického poľa. Sú to:
E – vektor intenzity elektrického poľa v jednotkách V.m–1,
B – vektor magnetickej indukcie v jednotkách T,
D – vektor elektrickej indukcie v jednotkách A.s.m–2,
H – vektor intenzity magnetického poľa v jednotkách A.m–1.
Tieto štyri vektory spolu s objemovou hustotou náboja ro(A.s.m–3) a objemovou prúdovou hustotou J (A.m–2) sú zviazané štyrmi Maxwellovymi rovnicami, ktoré predstavujú štyri základné zákony elektromagnetizmu. Na týchto zákonoch stojí celá stavba klasickej elektrodynamiky. Sú to nasledovné zákony – napísané slovne, v integrálnom a diferenciálnom tvare:
I. Gaussov zákon v elektrine: Tok vektora elektrickej indukcie D uzavretou plochou S sa rovná celkovému voľnému náboju Q uzavretému plochou S. Lokálnou vlastnosťou vektora D je skutočnosť, že jeho divergencia (výtok) v ľubovoľnom bode priestoru sa rovná objemovej hustote voľného náboja v tomto bode. Matematicky sú tieto vlastnosti elektrického poľa vyjadrené rovnicami
Z Gaussovho zákona napríklad plynie nepriamo úmerná kvadratická závislosť intenzity elektrického poľa bodového náboja od vzdialenosti a z to následne Coulombov zákon. Z Gaussovho zákona plynie dôležitá vlastnosť elektrického poľa, že je to pole zdrojové, tvorené elektrickými nábojmi. Je to potenciálové pole, podobne ako napr. gravitačné pole. Siločiary elektrického poľa sú orientované krivky začínajúce na kladných nábojoch a končiace na záporných
II. Gaussov zákon v magnetizme: Tok vektora magnetickej indukcie B uzavretou plochou S sa vždy rovná nule. Lokálnou vlastnosťou magnetického poľa je skutočnosť, že jeho divergencia z ľubovoľného bodu priestoru sa rovná nule. Matematicky sú tieto vlastnosti magnetického poľa vyjadrené rovnicami
Magnetické pole je nezdrojové, solenoidálne pole. Jeho pôvod súvisí s pohybom elektrických nábojov a jeho indukčné čiary sú uzavreté krivky. To zároveň svedčí o tom, že magnetické pole nemá zdroje v zmysle nejakých magnetických množstiev (magnetických nábojov).
Tu treba upozorniť, že Gaussov zákon by sa nemal zamieňať s Gaussovou vetou, ako sa to často robí v slovenskej literatúre, ktorá ešte stále býva ovplyvnená zlými prekladmi z ruskej literatúry. Zatiaľ čo Gaussov zákon (Gauss´ Law, Gaußsches Gesetz) je fyzikálny zákon (pozri napr. „Elektromagnetizmus“, kap. 2.4 a ďalej), Gaussova veta (Gauss´ Theorem, Gaußscher Satz) je matematická poučka (pozri napr. „Elektromagnetizmus“, kap. 2.6), pomocou ktorej možno, za istých podmienok, zameniť objemový integrál vektorovej funkcie súradníc na integrál plošný, tej istej funkcie, po ploche, ktorá daný objem obopína.
III. Faradayov zákon: Indukované elektromotorické napätie na uzavretej krivke l vo voľnom priestore, v dielektriku alebo vo vodiči sa rovná zápornej časovej zmene indukčného toku ľubovoľnou plochou S ohraničenou krivkou l. Lokálnou vlastnosťou poľa je skutočnosť, že rotácia intenzity elektrického poľa E v ľubovoľnom bode priestoru sa rovná zápornej časovej zmene vektora magnetickej indukcie B. Matematicky sú tieto vlastnosti elektromagnetického poľa vyjadrené rovnicami
Podľa Faradayovho zákona každá časová zmena magnetického poľa v nejakej oblasti, v ktorej leží uzavretá slučka l (myslená, alebo vodivá) vytvára na nej elektromotorické napätie, prípadne indukuje v nej elektricky prúd, ktoré spĺňajú zákon zachovania energie (pozri úvahu 21). Nie je dôležitý dôvod zmeny magnetického toku slučkou: pri stálom magnetickom poli môže to byť ľubovoľný pohyb slučky, jej otáčanie alebo deformácia tvaru. V pevnej slučke vyvolá elektromotorické napätie akákoľvek vnútorná časová zmena magnetického poľa. Táto variabilita príčin vzniku elektromotorického napätia a prúdu ústí vo veľkom počte praktických aplikácii Faradayovho zákona.
IV. Ampérov zákon: Magnetomotorické napätie na uzavretej krivke l vo voľnom priestore, alebo v látkovom prostredí sa rovná celkovému voľnému prúdu I nábojov pretekaných ľubovoľnou plochou S ohraničenou krivkou l a celkovému posuvnému prúdu reprezentovanému plošným integrálom časovej zmeny vektora elektrickej indukcie D na ploche S. Lokálnou vlastnosťou poľa je skutočnosť, že rotácia vektora intenzity magnetického poľa H v ľubovoľnom bode priestoru sa rovná súčtu vektora prúdovej hustoty J tečúcich nábojov a prúdovej hustoty posuvného prúdu dD/dt. Matematicky sú tieto vlastnosti elektromagnetického poľa vyjadrené rovnicami
Ak v nejakej oblasti priestoru tečie elektrický prúd I a s časom sa mení intenzita elektrického poľa E, resp. elektrická indukcia D (inač povedané, ak v danej oblasti priestoru existuje vodivý aj posuvný prúd), potom v tomto priestore vzniká magnetické pole H, alebo B ako dôsledok hustôt obidvoch prúdov. Nestacionárne magnetické pole vzniká aj vtedy, ak v priestor existuje iba posuvný prúd. Bez platnosti tohto zákona by neexistovali elektromagnetické vlny.
V elektrostatike a v magnetostatike sú všetky časové derivácie rovné nule. Maxwellovým rovniciam a ich aplikácii je venovaná celá učebnica „Elektromagnetizmus“ uložená na tejto webovej stránke.
Vektory E a B sú zviazané s elektromagnetickými potenciálmi V a A vzťahmi
Základnými vektormi elektromagnetického poľa sú vektory E a B, pretože tie určujú elektromagnetickú (Lorentzovu) silu
Felmag = qE + qv × B,
ktorá pôsobí na náboj q pohybujúci sa v poli rýchlosťou v. Častica s relativistickou hmotnosťou m sa v takomto silovom polí bude pohybovať podľa Newtonovej pohybovej rovnice
kde
je relativistická hybnosť častice, m0 je pokojová hmotnosť častice a c je rýchlosť svetla vo voľnom priestore (vo vákuu).
*****
Poznámka: Ak k týmto základným zákonom elektromagnetizmu pridáme Newtonov zákon všeobecnej gravitácie v známom tvare
(Fgrav je gravitačná príťažlivá sila dvoch častíc s hmotnosťami m1 a m2, r je ich vektorová vzdialenosť, k = 6,67428.10-11 m3.kg-1.s-2 je gravitačná konštanta), potom v týchto pár riadkoch tejto úvahy je obsiahnutá celá klasická fyzika.
*****
Na rozhraní dvoch látkových prostredí 1 a 2 platia pre vektory E1,2, D1,2, B1,2, a H1,2 hraničné podmienky
kde sigma je plošný náboj na rozhraní v jednotkách C/m2, Js plošný prúd rozhraním v jednotkách A/m a n0 je jednotkový vektor smerujúci kolmo z prostredia 1 do prostredia 2.
Rovnice pre hraničné podmienky matematickým spôsobom vyjadrujú skutočnosti, že na rozhraní dvoch prostredí tangenciálne zložky (Et1,2) vektorov E sú rovnaké a normálové zložky (Bn1,2) vektorov B sú takisto rovnaké. Normálové zložky (Dn1,2) vektorov D sa prechodom cez rozhranie menia o hodnotu hustoty náboja (sigma) na rozhraní a tangenciálne zložky (Ht1,2) vektorov H sa menia o hodnotu plošnej hustoty prúdu Js, ktorý v rovine rozhrania tečie kolmo na smer Ht1,2. Ak na rozhraní nie sú náboje, a teda netečú ani prúdy, potom na rozhraní aj normálové zložka Dn1,2a tangenciálne zložky Ht1,2 sú rovnaké (to je stredoškolská formulácia hraničných podmienok). Hraničné podmienky sú priamym dôsledkom platnosti Maxwellovych rovníc.
V látkových izotropných prostrediach sú vektory E, D, B a H viazané materiálovými vzťahmi
epsilon0 je elektrická konštanta (permitivita voľného priestoru – vákua), epsilonr je relatívna permitivita prostredia, µ0 je magnetická konštanta (permeabilita voľného priestoru – vákua) a µr je relatívna permeabilita prostredia. Parametre epsilonr a µr sú bezrozmerné látkové parametre a môžu byť číslami (pre lineárne, izotropné prostredia), tenzormi (pre anizotropné prostredia), alebo môžu závisieť od E, príp. B (v nelineárnych prostrediach).
Magnetická konštanta (permeabilita voľného priestoru – vákua) má presnú, definičnú hodnotu
µ0 = 4pi.10–7 H.m–1
pi = 3,14159..... je Ludolfovo číslo.
Elektrická konštanta (permitivita voľného priestoru) má číselnú hodnotu
kde
c = 299 792 458 m.s–1
je rýchlosť svetla vo voľnom priestore (vo vákuu).
Elektromagnetické pole sa v prírode najčastejšie vyskytuje vo forme elektromagnetických vĺn. Vo voľnom priestore sú to dve ortogonálne polia, v ktorých elektrické a magnetické vektory sú na seba navzájom kolmé a ležia v rovine kolmej na smer ich šírenia [je to transverzálna (priečna) elektromagnetická (TEM) vlna - pozri napr. "Elektromagnetizmus", kap. 11] . Pomer ich amplitúd spĺňa jednoduchý vzťah
Tento dôležitý parameter elektromagnetických vĺn sa nazýva vlnová impedancia voľného priestoru. Je to prírodná konštanta podobne ako rýchlosť svetla, hoci teoretickí fyzici ju takmer nespomínajú (možno preto, že mnohí ešte aj dnes pracujú v CGS-sústave a nie sú ani dodnes ochotní prijať SI-sústavu - pozri úvahu 12). Pojem impedancie Z sa takto okľukou vracia z elektrotechniky, kam sa dostal prostredníctvom Ohmovho zákona, do teórie elektromagnetického poľa.
V elektromagnetickom poli sa materiál elektricky a magneticky polarizuje. Vektory (prípadne tenzory) elektrickej polarizácie P (C.m-2) a magnetizácie M (A.m-1) sú dané výrazmi
kde
sú bezrozmerná elektrická a magnetická susceptibilita, ktoré môžu byť tenzory. V odporovo lineárnych prostrediach platí Ohmov zákon (diferenciálny tvar)
V tomto prípade sigma je konduktivita (S.m-1) a ro = 1/sigma je rezistivita materiálu (ohm.m). Môžu to byť tiež tenzorové veličiny.
Elektrické náboje sa v prírode zachovávajú, čoho matematickým vyjadrením je rovnica kontinuity elektrického prúdu
Podľa rovnice kontinuity prúd tečúci uzavretou plochou S sa rovná časovému úbytku náboja Q uzavretého plochou alebo v ľubovoľnom bode prúdového poľa sa divergencia prúdovej hustoty rovná časovému úbytku hustoty náboja r. V stacionárnych prípadoch sú derivácie rovné nule, tj. náboj Q v uzavretej ploche S a nábojová hustota ro v bodoch priestoru sa rovnajú nule, alebo zostavajú v čase konštantné.
V elektromagnetickom poli je sústredená energia s objemovou hustotou (J/m3)
a tečie priestorom s výkonovým tokom
S = E × H,
vo W/m2, čo je známy Poyntingov vektor.
*****
Je pozoruhodné ako málo zákonov a matematických rovníc, ktoré sme tu uviedli, tvorí teoretický základ elektromagnetizmu a dokonca celej fyziky (ak uvážime aj Newtonov gravitačný zákon). Ani hraničné podmienky nepatria do tohto súboru, pretože plynú z Maxwellových rovníc aplikovaných na rozhranie dvoch prostredí a uvádzame ich tu iba preto, že sú súčasťou takmer každého jednoznačného praktického riešenia elektro-magnetických úloh. Rovnica kontinuity (spojitosti) elektrického prúdu sa tiež formálne dá jednoducho odvodiť z Maxvellových rovníc, ale keďže vyjadruje zákon zachovania elektrického náboja, iba konštatujeme, že táto rovnica je konzistentná s Maxwellovými rovnicami. Nemôžeme predsa odvádzať jeden prírodný zákon (zákon zachovania) z iných zákonov!
Na prvý pohľad by sa zdalo, že fyzika je triviálna veda, že sa stačí naučiť niekoľko rovníc a každý v nej môže pracovať a dosahovať vedecké výsledky. Skúsenosť nás učí, že vždy to bolo inač a inač je to aj dnes. Tým rovniciam treba predovšetkým hlboko rozumieť a až na ich základe sa začína tvrdá práca fyzikov a inžinierov, ak sa úžitok z nich má preniesť do praxe. Ako sa to fyzike a technike darilo a darí, a začo všetko (v dobrom aj zlom) ľudstvo vďačí fyzike, vidíme zo súčasného stavu technického pokroku. Želám Vám pekný deň! Autor
08. 05.2009
25. Po roku!
Vážení priatelia!
Môžem s potešením konštatovať, že táto webová stránka prežila už jeden rok a za tú dobu bola navštívená viac než 7000 krát. Mám z toho dobrý pocit, že fyzika medzi vedami predsa ešte nie je úplnou „popoluškou“ a že ľudí, ktorí chcú a sú ešte schopní rozmýšľať je stále dosť (veď prečo ináč by v takej „gigaknižnici“, akou je internet vyhľadávali stránky s fyzikálnou problematikou – ale je to samozrejme relatívne). Tým, ktorí to robia to určite prináša uspokojenie a radosť z poznania zákonov, ktoré sú trvalé, ktoré nie sú výplodom ľudskej vôle, ktoré nezávisia napríklad od politickej situácie, ale sú odrazom pravdy, nezávislej od vedomia (pojem, ktorý s pojmom "bytie" radi nezmyselne konfrontovali marxistickí filozofi).
V tejto „výročnej“ úvahe by som chcel načrtnúť niektoré problémy, s ktorými sa dnes fyzika ako vedecký odbor potýka. Najprv sa zastavím pri súčasnom stave vzdelávania na všetkých stupňoch a to nielen vo fyzike, ale všeobecne. Myslím si, že mám na to právo, pretože v škole ako učiteľ som prežil polstoročie a tak môžem porovnávať.
O absolventoch fyziky voľakedy bolo známe, že sú schopní pracovať (ak samozrejme chcú) prakticky v ľubovoľnej oblasti ľudskej činnosti, ale naopak to neplatilo. Mnohí z tých, ktorých som učil, dnes pracujú na významných vedeckých pracoviskách (a nielen fyzikálnych) po celom svete. Krátko po „nežnej revolúcii“ som mal možnosť dva semestre prednášať fyziku vo vtedajšom Západnom Nemecku (SRN). Bol som prekvapený, keď som zistil, že úroveň vedomostí mladých Nemcov je značne nižšia ako úroveň vedomostí mojich bratislavských študentov (o Bratislave, ba ani o Pressburgu Nemci nevedeli ani kde sa nachádza). Dnes sa z médií dozvedám o nelichotivom postavení našich žiakov v rôznych – aj medzinárodných – monitoringoch vedomosti a to nielen v prírodných vedách, ale aj napríklad v jazykoch či v histórii. Príčiny tohto smutného stavu vidím v posunutí predstáv o hodnotách – od vzdelanosti, šľachetnosti, úcty k morálke a pravde, skôr k honbe za materiálnymi statkami, ku karierizmu, ku konzumu a k tolerancii klamstva. Škola, od ktorej by sa pri dnešných multimediálnych možnostiach čakalo, že bude žiakov a študentov stimulovať a orientovať k poznávaniu prírodných a mravných zákonov, musí vypisovať rôzne projekty aby prežila a obetaví učitelia, ktorí voľakedy trávili celé dni so študentmi v laboratóriách a v kabinetoch sa dnes boja vstúpiť do triedy, pretože nie sú si istí, či z nej po hodine vyjdú živí. Niektorí rodičia ako aj spoločnosť v tomto sizyfovskom zápase o vzdelávanie mladých napodiv nestoja vždy na strane učiteľov.
Druhá otázka, ktorá ma trápi, je akceptácia fyziky v spoločnosti. Dnes mnohé takzvané celebrity v rôznych interview veľmi radi a pyšne vyhlasujú akými nemožnými boli v škole v predmetoch ako je matematika a fyzika, až sa možno domnievať, že považujú za svoju prednosť, že nepatria do skupiny „kockatých“ hláv a že sú hlúpi a nevzdelaní. Možno by bolo pre ich popularitu lepšie neupozorňovať na tento svoj handicap, pretože ani pre skutočného "guru" nemôže byť ľahostajné poznanie toho, na čom vesmír funguje, naopak môže mu to napríklad pomôcť lepšie napĺňať a prežívať jeho umelecké kreácie. Aj medzi nimi existujú vzácne výnimky – napríklad herečka pani Kronerová, ktorá o sebe v jednom televíznom rozhovore prezradila, že ešte aj dnes vie riešiť systémy algebrických rovníc o dvoch neznámych. Považujem to za veľmi sympatické a zvyšuje to u mňa úctu k jej umeniu. Treba mať na pamäti, že mienka umelcov značne ovplyvňuje myslenie spoločnosti, hlavne mladých, preto by mala stimulovať pozitívny vzťah k vzdelaniu.
Tretia otázka je postavenie fyziky vo vedeckom svete. Voľakedy dávno nám náš učiteľ hovoril, že vedami v pravom slova zmysle sú len matematika a fyzika a všetko ostatné, čo sa vydáva za vedy sú v lepšom prípade náuky, v horšom iba pavedy. K takému vyjadreniu učiteľa viedla skutočnosť, že iba matematika a fyzika pracuje s exaktnými zákonmi, overenými stáročiami. Dnes s jeho názorom vôbec nemôžem súhlasiť, pretože úspechy, ktoré za posledných päťdesiat rokov dosiahli biológia, genetika, chémia a tiež relatívne nová veda – informatika, ich plným právom radia medzi vedecké disciplíny s veľkým aplikačným potenciálom. Jedno je však isté – či si to tieto vedy chcú, alebo nechcú priznať – vedami sa stali až vtedy, keď začali používať matematicko-fyzikálne metódy, ako aj zložité fyzikálne prístrojové zariadenia a tak prešli od opisného spôsobu poznávania sveta k analytickému.
Fyzika a matematika sú teda skutočne motorom ľudského pokroku a zaslúžia si v dnešnom svete primeranú pozornosť. Investície do ich rozvoja určite nebudú stratené.
Zatiaľ Vám želám pekné dni, a ak sa vyskytne niečo, čo bude stáť za reč, dovolím si znovu sa k Vám prihovoriť. Autor
10. 05.2009
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
